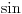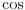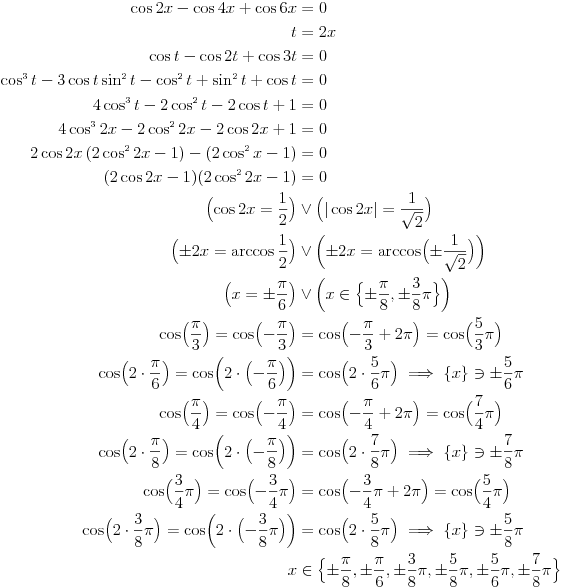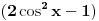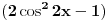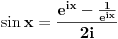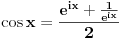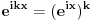[ Ruza79 @ 25.05.2009. 06:25 ] @
| Zamolio bih Vas sve za "malu" pomoć. Trenutačno sam student na PMF-u u Sarajevu i kroz čitav studij sam imao tu sreću da neka zaobiđem temu "trigonometrija". Iskren ću vam biti i reći da me je stvarno sram ali šta se može. Dali bi mi neko mogao pomoći u vezi trigonometriskih funkcija, način izrade zadataga kao i da mi da par korisnih savjeta kako se to uopće radi. Trigonometrija mi je jaaaaaako slaba strana i nemojte se ljutiti što ću možda nekada nešto i lupiti. Unapred vam zahvalna!!!!!! |