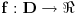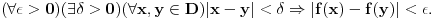Znači da zavisi samo od , a ne i od .

_{[Ovu poruku je menjao Nedeljko dana 01.06.2009. u 22:02 GMT+1]}

Da! Hvala, Nedeljko!

Uniformna (ravnomerna) neprekidnost znači da razlika |f(x1) - f(x2)| mora biti manja od epsilon nezavisno od izbora tačaka na datom skupu pod uslovom da je |x1 - x2| manje od delta. Uniforma neprekidnost je pojam globalnog karaktera, pa se odnosi na ceo skup za razliku od neprekidnosti u tački. Uniformna neprekidnost govori o osobini funkcije da na datom skupu, za bilo koji par tačaka, koje su na manjem rastojanju od delta, vrednosti funkcije se razlikuju za manje od datog epsilon.

Priraštaj funkcije je isti za isti priraštaj nezavisne promenljive (po apsolunim vrednostima).

Kod uniformne neprekidnosti delta zavisi samo od epsilon. Ako se posmatra grafik krive G:y=f(x) funkcije f:D->R, tada: funkcija f je uniformno neprekidna na D ako i samo ako za svako epsilon veće od nule postoji delta veće od nule tako da pravougaonik čije su stranice epsilon (vertikalna) i delta (horizontalna) i ako pri translaciji ovog pravougaonika "duž krive G" njegove horizontalne strane ni jednom ne seku krivu G.

Ako funkcija nije uniformno neprekidna to znači da postoji epsilon veće od nule tako da za svako delta veće od nule postoje x1 i x2 iz datog skupa i |x1 - x2| manje od delta povlači |f(x1) - f(x2)| veće ili jednako epsilon.

Hvala i tebi, holononi, sad je sve jasno.

Primer:
f(x) = 1/x je na intervalu (0,1] neprekidna ali nije ravnomerno (uniformno neprekidna)