Kako važi

φ_X(t) = E( cos(tX) + i*sin(tX) ) = E( cos(tX) ) + i*E( sin(tX) )

tada je

φ_X(t) = E( cos(tX) )

za tX = 0, Pi, 2*Pi, ...

Vidim holononi u poslednje vreme da umeš da budeš koristan ljudima. Ovo kažem da ne bi pomislio da te samo nešto kritikujem. Samo se ograniči na ono što zaista znaš i super si.

E da, nisam dobro objasnila sta mi treba jer usvari nemam pojma. Zato uceci dalje, mislim da cu formulisati bolje pitanje. Ono sto citam je random walk. za binomnu raspodelu karakteristicna funkcija je (q+pexp(t)) za jedan korak. e ono sto meni nije jasno kako je to onda jednako cos (kY) Y je duzina koraka.

ustvari da je q+pexp(ik)=cos(kY)

@Nedeljko
Drago mi je da ima onih koji se sekiraju za mene. Koliko blistam od zadovoljstva ni sijalicu ne palim u mraku. Samo da bljesak nekome ne natera suze u oči pa plaču kod moderatora.


@Karakteristična funkcija
Ako je u pitanju simetričan random walk na pravoj onda



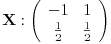
φ_X(t) = Ee^itx = (1/2)e^it(-1) + (1/2)e^it(1) = (1/2)( e^-it + e^it ) = cos( t )

jer je E( X ) = Suma( x_kP(x_k) ), k=1,2,...,n, kao i

e^it = cos( t ) + i*sin( t )
e^-it = cos( t ) + i*sin( -t ) = cos( t ) - i*sin( t ) (sinus je neparna funkcija)

Sabiranjem ove dve jednakosti se dobije

e^it + e^-it = cos( t ) + i*sin( t ) + cos( t ) - i*sin( t ) = 2 cos( t )


Inače za binomnu slučajnu promenljivu, Sn = I₁ + I₂ + ... + I_n karakteristična funkcija je

φ_Sn(t) = Ee^{it(I1+...+In)} = E( e^itI1e^itI2...e^itIn ) = E( e^itI1 )*E( e^itI2 ) * ... * E( e^itIn ) = φ_I1(t)*φ_I2(t)* ... *φ_In(t) = (1 - p + pe^it)ⁿ

pa se za n = 1 dobije φ_X(t) = q + pe^it, jer je za



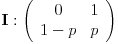
φ_I(t) = Ee^itI = e^it*0(1 - p) + e^it*1p = 1 - p + pe^it

E sad je jasno.:-) Hvala ti mnogo. Mnogo si mi pomogao i dao lepo objasnjenje. Btw, postavicu ja jos koje pitanje. Pa da mi budes pri ruci ako je to moguce;-)

veliki pozdrav

U opstem slucaju karakteristicna funkcija je inverzna fourier-ova transformacija funkcije gustine raspodele.
Funkcija gustine raspodele za diskretnu slucajnu promenljivu pokazuje verovatnocu pojavljivanja slucajne promenljive u izvesnim diskretnim vrednostima P(X=k) i njoj odgovara periodicna funkcija u vremenu (karakteristicna funkcija).