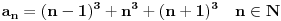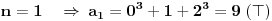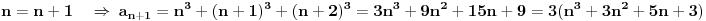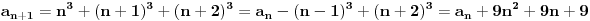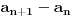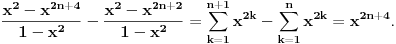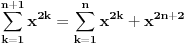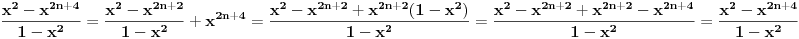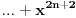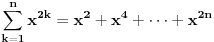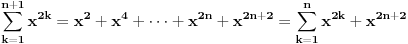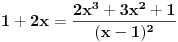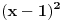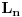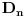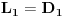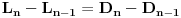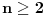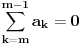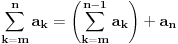[ plotter @ 20.06.2009. 19:33 ] @
|
[ plotter @ 20.06.2009. 20:14 ] @
Jel moze malo pojasnjenje, posebno ovog dela
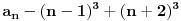 , odnosno kako si dosao do toga? , odnosno kako si dosao do toga?Evo jos jedan sa indukcijom iz osobina celih brojeva... Ovaj ne znam ni kako da zapocnem, neki hint ili postupak bi mi bio od velike pomoci: 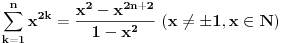 Takodje bi mi od pomoci bio neki link ili literatura koja je vama pomogla da savladate matematicku indukciju. [ japan @ 20.06.2009. 20:52 ] @
Citat: plotter: Jel moze malo pojasnjenje, posebno ovog dela 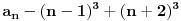 , odnosno kako si dosao do toga? , odnosno kako si dosao do toga?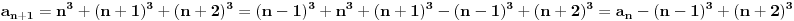 Citat: isto indukcijom, treba da dokazes da je 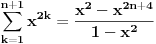 hint za indukcijski korak: 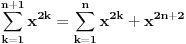 generalno, oko indukcije nema mnogo mudrosti - dokazes da nesto vazi za bazu indukcije (pocetni korak), pretpostavis da vazi za neko n, a onda, koristeci tu pretpostavku, treba da dokazes da vredi i za n+1. tu sad ponekad treba malo vestine i moci zapazanja, ali do toga se lako dolazi vezbom, od od laksih primera, kao sto je ovaj prvi, pa ka tezim. [ Nedeljko @ 20.06.2009. 21:32 ] @
[ plotter @ 21.06.2009. 01:01 ] @
[ japan @ 21.06.2009. 12:03 ] @
[ plotter @ 21.06.2009. 12:28 ] @
Jeste, hvala svima.
[ plotter @ 22.06.2009. 21:06 ] @
Uzeo sam da vezbam zadatke iz udzbenika"Visa Matematika" izdatog '71 i ne ide lose za sada, odradio sam par prostih primera bez vecih problema.
U medjuvremenu sam naisao na jedan problem koji ne mogu da resim maltene ni za n=1, pa vas molim za pomoc: 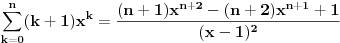 Siguran sam da postoji "catch", ja se zaglavim negde u elementarnoj algebri [Ovu poruku je menjao plotter dana 24.06.2009. u 21:34 GMT+1] [ Nedeljko @ 23.06.2009. 08:06 ] @
[ plotter @ 24.06.2009. 20:45 ] @
U pravu si za minus, ispravio sam zadatak.
Ja ocigledno postavku ne shvatam najbolje, molim te pomozi mi: k=0, znaci brojimo od 0. Kada kazemo da je n=1, to znaci da u nizu ima n elemenata - na primer 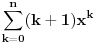 je za n=1 jednaka je za n=1 jednaka 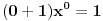 (ova jedinica je taj jedan element) (ova jedinica je taj jedan element)Da li kada je k=0 mi u nizu imamo n=1 ili n=0 elemenata? [ zzzz @ 25.06.2009. 00:49 ] @
plotter: "Da li kada je k=0 mi u nizu imamo n=1 ili n=0 elemenata?
Izgleda da ti nije jasno šta znači izraz suma (grčko sigma).To ti je zbir članova kojih ima koliko i k-aova.Pa ako je početno k=0,a najveće k=3 (a to je onda kad je n=3) onda imaš četiri člana u toj sumi.Prvi za k=0,drugi za k=1,treći za k=2 i četvrti za k=3.Za svaki od ovih k-ova izračunaj vrijednost izraza i onda ih sve saberi. Naprimjer za n=1 suma je (1)+(2x)=1+2x jer je za k=0 izraz jednak 1,a za k=1 je 2x.Ako bi n bilo 2 onda bi dodao još jedan sabirak (tri iks na kvadrat). [ Nedeljko @ 25.06.2009. 07:48 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|