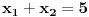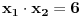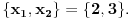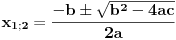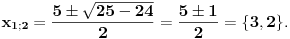[ vlajko80 @ 25.06.2009. 12:23 ] @
| Jel moze neko da me uputi kako da pomocu vijetovih formula nadjem resenja kvadratne jednacne ?? Npr.. x^2-5*x+6=0 na osnovu x1+x2=-b/a i x1*x2=c/a je x1+x1=5 x1*x2=6 i dalje ne znam. Kapiram kako da na osnovu resenja formiram jednacinu ali ocigledno ne i suprotno. Pokusao sam Keckica,Ognjanovica,Venea...ali nigde nisam nasao primer ovog tipa. Uglavnom se odredjuju neki realni parametri, koeficijenti...ili ako se traze resenja kv.jed. dati su josh neki uslovi. Molim moderatora da mi ovaj put ne brishe temu !!!!!! Hvala!:) |