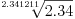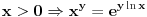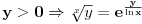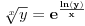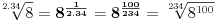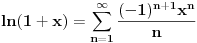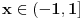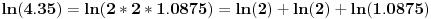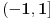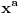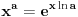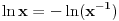Da li ti je ovo dovoljno dobro za tvoj program

, ?

Zar nije ?

Nisam se setio ovog nacina

Pokusacu, mozda uspem

Tako je, bila je moja greška.

Ok, hvala ti

E sad kad sam razmislio shvatio sam da ne moze ovaj nacin

Opet nemam onaj ceo broj n(n-ti koren) kojim bi preko neke metode (Njutnove) racunao.

Mogu ja da transformisem npr:



Ali sta ako dobijem 2.112233445566 to je vec 8 na 1000000000000 tako da kompjuter to nece moci da izracuna....

Ahaaaaa sad sam skontao

Taj e na nesto mogu lako da razvijem u red ))

Hvala!

Pa zar nemaš u standarnoj biblioteci funkcije log i exp? Ovu formulu možeš direktno da primeniš.

Da da znam. Hocu da napravim svoju biblioteku sa ovim operacijama ali sa mogucnoscu da radi sa velikim brojem decimalnih mesta.

Kao na primer: http://www.alpertron.com.ar/BIGCALC.HTM

Jos nesto me zanima, kako da razvijem ln u red?

Npr: ali za svako

Kako sad da razvijem ako x nije u ovom opsegu?

Ja sam razmisljao na ovaj nacin:

Npr: I sa ovim ln(2) mogu da razvijam u red jer je tad x=1.


Da li postoji razvijanje u red logaritma ako je x van ovog opsega

Resio sam problem sa logaritmom.

A sto se tice n-tog korena, skroz sam zaboravio na razvoj funkcije u red

Sve zavisi od reprezentacije broja koju koristiš. Ako koristiš oblik mantisa, eksponent, tj. x=2^Em, onda ti je m u intervalu [1/2,1) i ln(x)=-E*ln(1/2)+ln(m). Sa druge strane, za svako x>0 i t=(x-1)/(x+1) je |t|<1, pa možeš koristiti formulu

.

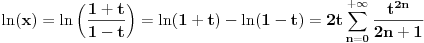Ovo uvek konvergira.

No, toplo ti preporučujem da pogledaš biblioteke gmp i mpfr. Ljudi su se već bavili takvim stvarima, pa bi mogao da pogledaš algoritme u dokumentaciji. Smatraj da su ugrađeni algoritmi praktično najbrži poznati algoritmi, tako da bilo koji pomak da napraviš, značajan je.

.

Ovako možeš slučaj x>1 da svedeš na slučaj x<1:
.

Ok,hvala ti. Pogledacu one biblioteke.