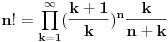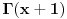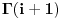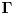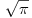To znaju samo:

1) Programeri koji su pravili calc.exe

2) Oni koji debaguju calc.exe, recimo u SoftIce-u

Pogledaj npr. (uopšteni faktorijel):

http://www.efunda.com/math/gamma/index.cfm

takođe pogledaj:

http://www.elitesecurity.org/t136880-0

Pa, obzirom da je , izgleda da je u pitanju funkcija .

Hm, koliko li je i! ?
( i je imaginarna jedinica, i*i = -1 )

Pa, valjda se zna sta je .

-funkcija je definisana u celom kompleksnom podrucju osim u celobrojnim nepozitivnim tackama.

Nije sporno da je gama-funkcija uopštenje faktorijela, ali to ovde nije tema. Pitanje je bilo koja formula se koristi u algoritmu koji je upotrebljen za izračunavanje faktorijela u programu calc.exe.

U tom programu (Windows-ov kalkulator) sam izračunao (-0.5)! i dobio .

Da da i ja sam juce citao nesto o gama funkciji.

Verovatno se preko nje radi.

U pravu je Nedeljko (-0.5)! je bas koren iz pi, tako kaze win calc.

Nego imam jednu zanimljivost,nevezano za ovu temu, kada sam u programu Maple trazio da mi program izracuna korene kubne jednacine: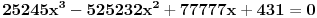


Dobio sam resenja: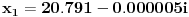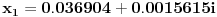





Kao prvo treba da ima jedno realno resenje, nema ga.
Kao drugo ako ima kompleksna moraju biti i konjugovana, nisu.

U cemu je ovde fora??

Windows-ov kalkulator zadovoljava i jednakost 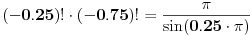, a takodje je za vrednosti x bliske nuli (x-1)!~1/x.

Kod numeričkog rešavanja jednačina treba imati na umu da su dobijena rešenja približna, što se odnosi i na realni i na imaginarni deo. Verovatno su sva tri rešenja realna, a imaginarni deo je samo deo numeričke greške.

Pa lepu gresku pravi

Inace, ja sam uspeo da napravim program za racunanje korena polinoma bilo kog stepena (realna+imaginarna) i nemam takvu gresku

A da li garantuješ tačnost, tj. da je tačno rešenje u nekom opsegu?

Ja se nadam da mi je, solidno, tacno.

Uporedjivao sam i sa drugim programima i dobijaju isto kao i ja.

Koristio sam Lin-Bairstow metod sa prelazima od 10000 puta mada vec posle 20-ak prelaza dobijem resenje.

Evo postavio sam prog koji racuna samo treceg stepena (koristeci Njutnov metod - isto broj prelaza je 10000).

Kraj programa je kada se za vrednost "a" ucita 0.

Program je malo neuredan, jer nisam stigao da ga malo sredim.

Vidim da tamo ispaljuješ 50 cifara. Da li si siguran da su sve prikazane cifre tačne?

Ne znam, ne mogu da garantujem, odnosno nemam gde da proverim. Eto mogu da kazem da je bar 10-ak 15 cifara (iza decimalne tacke) tacno.

Kazem ti koristio sam Njutnov metod i imao sam 10000 prelaza, znaci dosao sam do

Nakon ovoliko prelaza mora da sam dobio dosta precizno resenje.

Ograničenost tačnosti računa ograničava tačnost dobijenog rezultata, koliko god ti iteracija primenio.

Ako bi da radiš, mogu ti reći algoritam kojim dobijaš rezultat u garantovanom opsegu. Dakle, moguće je napisati program sa sledećim svojstvima:

1. Sve ulazne veličine su celi brojevi i kompleksni brojevi sa racionalnim realnim i imaginarnim delom.
2. Izlazne veličine su celi brojevi ili kompleksni brojevi dati preko intervala kome pripada realni ili imaginarni deo. Pripadanje realnog, odnosno imaginarnog dela rezultujućem intervalu je garantovano.
3. Program može prikazati rezultate u bilo kojoj željenoj tačnosti, to jest intervali kojima pripadaju realni, odnosno imaginarni deo izlazne veličine mogu biti uski onoliko koliko korisnik to traži.
4. Na ulazu se zadaju stepen polinoma i njegovi koeficijenti kao kompleksni brojevi.
5. Na izlazu se dobijaju sve različite kompleksne nule polinoma, pri čemu program za svaku ispisuje i njenu višestrukost, a ako je potrebno, neke nule može prikazati u većoj tačnosti da bi se razlikovale unutar te tačnosti. Drugim rečima, svi izlazni kompleksni zatvoreni pravougaonici su disjunktni.
6. Za pravu {x+iy : Ax+By=C} u kompleksnoj ravni, sa datim racionalnim koeficijentima A,B i C, (pri čemu ne može biti A=B=0) se može pouzdano utvrditi koje joj nule pripadaju, ako ima takvih. Posebno, može se dobiti tačan broj svih realnih nula polinoma sa kompleksnim koeficijentima.

Eto, to je ostvarivo.

OT:
sta je ovo . sve kolege pozurile s numerikom :) meni jos prosle godine trebao romberg i jos neke fore za nesto ...

bas sam s rombergom imao muka da izvucem potrebnu preciznost
(na CUDAi, daleko manju preciznos ima u odnosu na FPU ...)