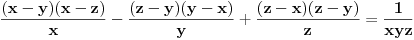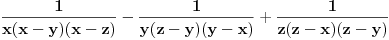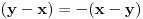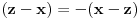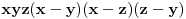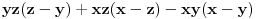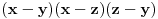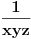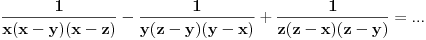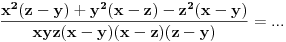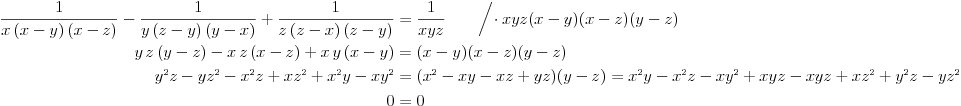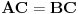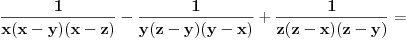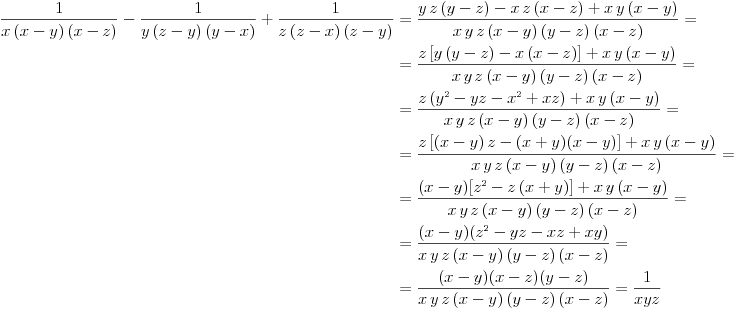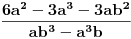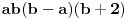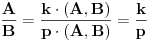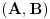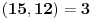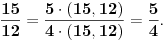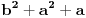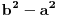[ vlajko80 @ 01.07.2009. 00:56 ] @
|
| Da li neko moze da mi pomogne oko sledeceg: Treba dokazati da je...
1/x*(x-y)*(x-z)-1/y*(z-y)*(y-x)+1/z*(z-x)*(z-y)=1/x*y*z
ja sam uspeo da doguram do...
x^2*(z-y)+y^2*(x-z)-z^2*(x-y) / x*y*z*(x-y)*(x-z)*(z-y)=......i dalje ne mogu :(
|
[ RMAN @ 01.07.2009. 01:21 ] @
Ako sam dobro procitao sta si napisao to je onda:
Treba pokazati da je:
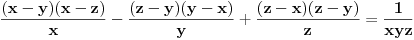
Neka je x=y=z=1
Tada je leva strana 0 a desna 1. Sto znaci da ovo i da hoces ne mozes doakzati da je tacno.
Znaci ova jednakost nije tacna. [ RMAN @ 01.07.2009. 01:41 ] @
A ne pogresno sam protumacio to sto si napisao, treba ti jos nekoliko zagrada.
znaci izraz 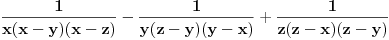
Malo transformises izraz tako sto ces izvuci minus ispred zagrada 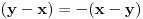 i 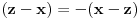
Nadjes im zajednicki: 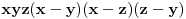
I kad saberes razlomke dobijas u brojiocu 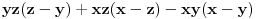
Ovo pomnozis svaki sa svakim kao i izraz 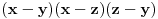 u imeniocu i videces da se oni mogu skratiti.
Posle skracivanja dobijas 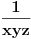 [ vlajko80 @ 01.07.2009. 02:44 ] @
pa vidish dotle sam i ja dogurao i nista se ne krati u brojiocu ...samo se zakomplikuje , vec sam to otkuco gore dokle sam stigao.
a ja bih rekao da imenioc ne treba diradi znaci da ostaje x*y*z*(x-y)*(x-z)*(z-y).
Mene samo muci ovo u brojiocu, najbolje sto sam uspeo da ga sredim je ovo x^2*(z-y)+y^2*(x-z)-z^2*(x-y)....
:((
Zapravo u brojiocu bi trebalo da se dobije (x-y)(x-z)(z-y) i onda se to krati sa imeniocem i onda ostaje \frac{1}{xyz}
ali ja nikako ne mogu to da izmajmunishem :((
[ Nedeljko @ 01.07.2009. 11:15 ] @
Pomnožiš sve sa xyz, izmnožiš sve i sve ti se pokrati. To je opšti slučaj kod dokazivanja jednakosti racionalnih izraza.
[ vlajko80 @ 01.07.2009. 11:47 ] @
Pa ako ga mnozim za xyz samo ga dizem za stepen vishe , gde je tu skracivanje ???
Ne, stvarno , ne kapiram :((((
[ Nedeljko @ 01.07.2009. 13:46 ] @
Pomnožiš yz(x-y)(x-z)=x2yz-xy2z-xyz2+y2z2 i tako dalje. Napišeš obe strane u obliku zbira monoma i moraju se poklopiti.
[ Nedeljko @ 01.07.2009. 13:50 ] @
Sad sam video tačan izraz. Znači, pomnožiš celu jednakost sa xyz(x-y)(y-z)(y-x) i ond arazviješ sve da dobiješ obe strane u obliku zbira monoma. To je opšti slučaj kod dokazivanja jednakosti racionalnih izraza.
[ vlajko80 @ 01.07.2009. 14:18 ] @
ja sam bash to hteo da izbegnem ,mislim da mnozim ceo razlomak sa xyz(x-y)(y-z)(y-x) / xyz(x-y)(y-z)(y-x) .
ali cek, kako mislis obe strane ???
Jer ja startujem od 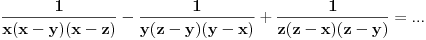
a znam da treba da se dobije 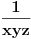 tako da sa desne strane jednakosti za sada nemam nista
ja sam uspeo da ga sredim do 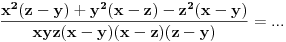 i dalje nemam ideju kako da ga sredjujem
a da dobijem 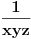 [Ovu poruku je menjao vlajko80 dana 01.07.2009. u 15:42 GMT+1]
[Ovu poruku je menjao vlajko80 dana 01.07.2009. u 15:46 GMT+1]
[Ovu poruku je menjao vlajko80 dana 01.07.2009. u 15:47 GMT+1]
[Ovu poruku je menjao vlajko80 dana 01.07.2009. u 15:55 GMT+1]
[Ovu poruku je menjao vlajko80 dana 01.07.2009. u 15:56 GMT+1]
[Ovu poruku je menjao vlajko80 dana 01.07.2009. u 15:56 GMT+1]
[Ovu poruku je menjao vlajko80 dana 01.07.2009. u 16:03 GMT+1]
[Ovu poruku je menjao vlajko80 dana 01.07.2009. u 15:42 GMT+1]
[Ovu poruku je menjao vlajko80 dana 01.07.2009. u 15:46 GMT+1]
[Ovu poruku je menjao vlajko80 dana 01.07.2009. u 15:47 GMT+1]
[Ovu poruku je menjao vlajko80 dana 01.07.2009. u 15:55 GMT+1]
[Ovu poruku je menjao vlajko80 dana 01.07.2009. u 15:56 GMT+1]
[Ovu poruku je menjao vlajko80 dana 01.07.2009. u 15:56 GMT+1]
[Ovu poruku je menjao vlajko80 dana 01.07.2009. u 16:03 GMT+1][ vlajko80 @ 01.07.2009. 14:21 ] @
A jel mozes ti , ako vec imas to negde uradjeno da mi posaljes na mail ili tako nesto , bio bih ti mnogo zahvalan!:)
Jel sada nesto razmisljam ako pomnozim i razvijem razlomak, nista nece moci da se skrati jel cu imati sabiranje i oduzimajne "monoma"
cilj je da se faktorise i onda skrati, po meni ....ne znam , sta vi mislite ....muci me ovaj problem:(( [ Cabo @ 01.07.2009. 15:22 ] @
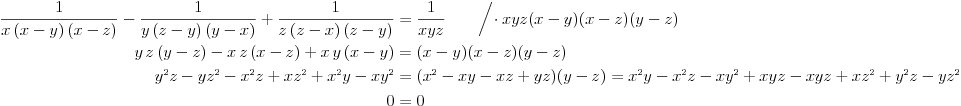
( Napomena: U prvoj jednakosti obe strane se množe istim izrazom, što je korektno. Na primer, iz izraza 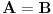 množenjem obe strane sa  dobijamo izraz 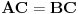 .)
[Ovu poruku je menjao Cabo dana 01.07.2009. u 16:51 GMT+1][ vlajko80 @ 01.07.2009. 16:00 ] @
E Cabo hvala puno, sila si.:))))))Naravno, zahvaljujem se i drugima!:)))) A da li mozes da mi pokazes kako da od 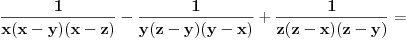
dodjem do 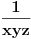 ???
To je ono sto trenutno pokusavam i ne ide mi ......
[ Cabo @ 01.07.2009. 16:19 ] @
Svođenjem na zajednički imenilac i faktorisanjem:
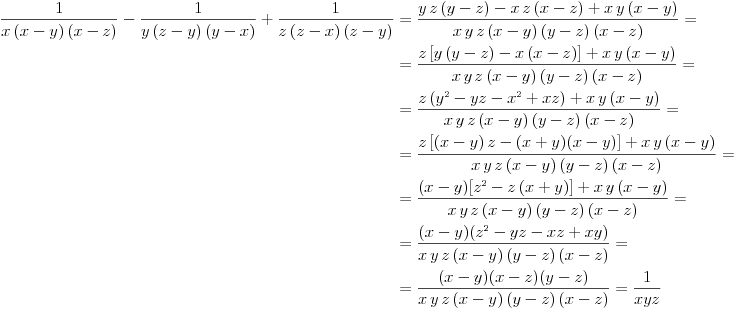 [Ovu poruku je menjao Cabo dana 01.07.2009. u 17:48 GMT+1]
[Ovu poruku je menjao Cabo dana 01.07.2009. u 17:48 GMT+1][ vlajko80 @ 01.07.2009. 16:50 ] @
cek da ja to pogledam .........
Odlicno , super .....bravo majstore ....mnogo si mi pomogao !:)
Hvala tebi i svima koji su se ukljucili u ovu temu !:))
Zaista ste sjajni, hvala josh jednom :))))
[ Cabo @ 01.07.2009. 17:01 ] @
Nema na čemu, drago mi je da sam ti pomogao.
[ vlajko80 @ 02.07.2009. 01:06 ] @
Drugari , opet sam zabagovao !?:(((
Imam izraz 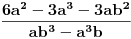 i to treba nekako skratiti.
Izraz u imeniocu mi nije problem i to bi bilo 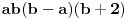 ali ovaj gore me muchi!
Jel ima neko ideju ???:)) [ Nedeljko @ 02.07.2009. 08:15 ] @
Jedan metod je da oba izraza "shvatiš" kao polinome po a (ili b), pa tražiš NZD. Kad ga izračunaš, ako ne budeš znao dalje, postavi rezultate, pa da vidimo dalje.
[ vlajko80 @ 02.07.2009. 11:53 ] @
Zaiisa ne kontam sta dobijam ako im nadjem NZD ??
Kapiram da postoji caka da se gornji izraz faktorishe ali ja ne znam kako :(
[ Cabo @ 02.07.2009. 12:04 ] @
Kako uopšte skraćuješ razlomke?
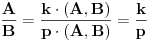
( 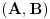 je NZD  i  .)
Na primer:
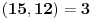
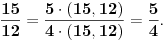 [ vlajko80 @ 02.07.2009. 14:26 ] @
hmmm...da to mi je jasno ali ne znam kako to da primenim na ovaj primer 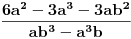 :((( [ Nedeljko @ 02.07.2009. 22:20 ] @
Prvo, jasno je da se razlomak može skratiti sa a, kao i da se iz brojioca može izvući -3, a iz imenioca može izvući b.
Nađimo NZD od 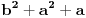 i 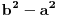 , kao polinoma po b.
Delenje daje daje količnik 1, a ostatak  . To znači da je NZD konstanta, jer ne zavisi od b, pa je dalje skraćivanje uzaludan posao. [ vlajko80 @ 03.07.2009. 15:37 ] @
hmm, pa da ...jasno ! hvala puno!:))
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|