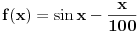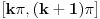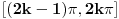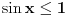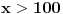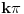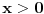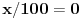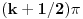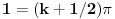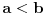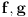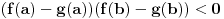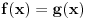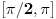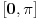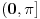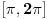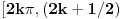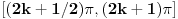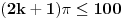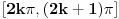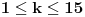Šta si ti odgovorio?

Da ima samo jedno rješenje. Tj. da je to rješenje nula... malo sam izfilozofirao, ali nisam uspio dokazati po cemu nema drugih resenja...Ali me cisto interesuje da li je moj odgovor tačan. Ako ima još koje da se džaba ne nadam!

Jesi probao napraviti graf te 2 funkcije.Mozes npr. ovdje http://www.walterzorn.com/grapher/grapher_e.htm vidjeti da ima jedno 64 rjesenja.

Ovako odokativno, sudeći po grafiku u Matematici vidim da ih ima bar jedno desetak. Zadatak je vraški postavljen. U suštini, ti treba da nađeš nule funkcije .

Ajme. Hvala u svakom slučaju...

Ukupan broj rešenja je 2N+1, gde je N broj pozitivnih rešenja. Zato ćemo odrediti samo broj N pozitivnih rešenja.

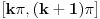
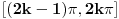
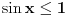
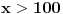
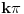
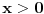
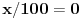
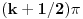
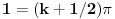
Ni na jednom od intervala oblika nema više od dva rešenja zbog konveksnosti/konkavnosti sinusa. Na intervalima oblika nema rešenja zbog nepozitivnosti sinusa. Iz sledi da za nema rešenja. Rešenja ne mogu biti oblika , jer za ne može biti , kao ni , jer bi onda bilo , a je iracionalan broj.

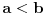
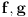
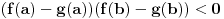
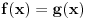
Takođe, ako je za neke ispunjeno da za neprekidne funkcije važi da je , onda na tom intervalu postoji barem jedno rešenje jednačine , a ako je pritom i jedna od tih funkcija rastuća, a druga opadajuća, onda je to rešenje jedinstveno na tom intervalu.

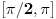
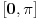
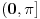
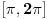
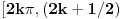
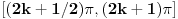
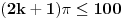
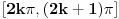
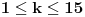
Na intervalu postoji rešenje, a pošto je 0 rešenja, a na intervalu ne može imati više od jednog rešenja, onda na intervalu postoji tačno jedno rešenje. Na intervalu nema rešenja. Rešenja ima na intervalima oblika i za , pa na intervalima oblika za ima po tačno dva rešenja, odakle je N=31 i konačno, ukupan broj rešenja je 63.

Hvala mnogo u svakom slučaju, ali ovo definitvno ne bih znao uraditi...

Ako može pomoš so ovaa zadača ve molam.
Treba da se proveri dali konvergira.




Blagodaram odnapred. :)

Koristi Kosijev kriterij za konvergenciju redova.

@ different

Fala za pomošta.Sea ќe probam. ;)