[ Nedeljko @ 19.07.2009. 09:27 ] @
| Pretpostavimo da je dato 5 tačaka u ravni. Dokazati bez upotrebe Paskalove ili Štajnerove teoreme da ne postoje dva nedegenerisana konusna preseka koja prolaze kroz tih 5 tačaka. |
|
[ Nedeljko @ 19.07.2009. 09:27 ] @
[ Cabo @ 19.07.2009. 16:26 ] @
Šta je dozvoljeno? Da li je ravan u projektivnom prostoru?
[ Nedeljko @ 20.07.2009. 07:31 ] @
Recimo, radi se u proširenoj euklidskoj ravni, a definicija konike je preko algebarske jednačine drugog reda.
[ Nedeljko @ 20.07.2009. 11:05 ] @
Evo, u čemu je stvar:
Najpre sam hteo da nađem algebarsku interpretaciju Paskalove teoreme i dokažem je na algebarski način. Radio sam u homogenim koordinatama. Uslov da vektor koji predstavlja tačku i vektor koji predstavlja pravu odgovaraju incidentnim objektima (tačka pripada pravoj) je zapravo ortogonalnost vektora homogenih koordinata (tačke i prave). Stoga se vektor koji predstavlja pravu kroz dve tačke može dobiti kao vektorski proizvod (u R3, gde leže vektori homogenih koordinata) vektora koji predstavljaju tačke, tj AB = A x B. Slično tome je presečna tačka pravih zapravo predstavljena vektorskim proizvodom vektora kojima su predstavljene prave. Uslov kolinearnosti triju tačaka i konkurentnosti triju pravij je jednakost mešovitog proizvoda nuli, tako da je algebarski zapis Paskalove teoreme 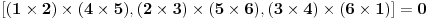 . .Odnosno nakon primene formula za dvostruki vektorski proizvod 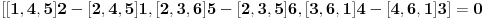 ili posle sređivanja (*) 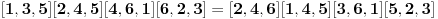 . .Dakle, ovu jednskost treba dokazati. Pretpostavimo da su tačke 1,...,5 fiksne, a da tačka 6 ima opšte koordinate 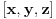 . (*) je algebarska jednačina najviše drugog reda po . (*) je algebarska jednačina najviše drugog reda po 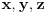 . Ona je ili trivijalna jednačina 0=0 (koja je svakako tačna) ili jednačina nekog konusnog preseka, degenerisanog ili nedegenerisanog. Lako se pokayuje da se zamenom tačke 6 bilo kojom od tačaka 1,...,5 dobija identitet, to jest, sve od tačaka 1,...,5 zadovoljavaju jednačinu (*), pa je (*) ili trivijalna jednačina 0=0 ili jednačina konusnotg preseka (degenerisanog ili nedegenerisanog), koji sadrži tačke 1,...,5. U slučaju degenerisane konike, među bilo kojih njenih pet tačaka mogu izabrati tri kolinearne, dok nedegenerisan konusni presek nema trojki kolinearnih tačaka. Stoga, pošto tačke 1,...,5 leže na nedegenerisanom konusnom preseku od koga smo pošli, među tačkama 1,...,5 nema triju kolinearnih, pa ako jednačina (*) nije trivijalna, onda je to jednačina nedegenerisanog konusnog preseka koji prolazi kroz tačke 1,...,5. Ukoliko je takav konusni presek jedinstven, onda je to naš polazni konusni presek, kome pripada i tačka 6, pa samim tim važi (*). . Ona je ili trivijalna jednačina 0=0 (koja je svakako tačna) ili jednačina nekog konusnog preseka, degenerisanog ili nedegenerisanog. Lako se pokayuje da se zamenom tačke 6 bilo kojom od tačaka 1,...,5 dobija identitet, to jest, sve od tačaka 1,...,5 zadovoljavaju jednačinu (*), pa je (*) ili trivijalna jednačina 0=0 ili jednačina konusnotg preseka (degenerisanog ili nedegenerisanog), koji sadrži tačke 1,...,5. U slučaju degenerisane konike, među bilo kojih njenih pet tačaka mogu izabrati tri kolinearne, dok nedegenerisan konusni presek nema trojki kolinearnih tačaka. Stoga, pošto tačke 1,...,5 leže na nedegenerisanom konusnom preseku od koga smo pošli, među tačkama 1,...,5 nema triju kolinearnih, pa ako jednačina (*) nije trivijalna, onda je to jednačina nedegenerisanog konusnog preseka koji prolazi kroz tačke 1,...,5. Ukoliko je takav konusni presek jedinstven, onda je to naš polazni konusni presek, kome pripada i tačka 6, pa samim tim važi (*).Zašto me ovo zanima? Pa, da bih pokušao da nađem uopštenja Paskalove teoreme, na primer za n-dimenzioni slučaj ili neka druga. [ Nedeljko @ 20.07.2009. 11:06 ] @
Ako je nekome lakše, može slobodno da koristi definiciju konusnog preseka preko polariteta.
[ Cabo @ 20.07.2009. 14:20 ] @
Čisto da se javim da sam skinuo tvoj odgovor na fleš, pa ću ga pogledati kod kuće.
[ Cabo @ 21.07.2009. 17:17 ] @
Može li se koristiti Štajnerova definicija krive drugog reda? Kako glasi definicija preko polariteta?
Koliko sam shvatio, cilj je pokazati da je kriva drugog reda incidentna sa 5 tačaka jedinstvena. [ Nedeljko @ 22.07.2009. 08:00 ] @
Ja sam itekako pozaboravljao ove stvari, ali ako izvedeš Štajnera iz polariteta, onda može da se koristi, ali mi u tom slučaju ništa ne znači bez dokaza Štajnera.
[ Cabo @ 22.07.2009. 15:27 ] @
Malo podsećanje:
Definicija (Štajner): Kriva drugog reda je skup presečnih tačaka parova odgovarajućih pravih dvaju pramenova, među kojima je uspostavljeno projektivno preslikavanje. [ Nedeljko @ 22.07.2009. 20:58 ] @
Ma, meni je bitan sadržaj. OK, ako prihvatimo tu definiciju, onda dokaži da je skup samokonjugovanih tačaka bilo kog polariteta zadovoljava i dalje dokaži iz te definicije da je konusni presek kroz pet tačaka jedinstven.
[ Cabo @ 24.07.2009. 16:46 ] @
Baš ovih dana spremam usmeni iz Nacrtne. Ali još nisam došao do tog dela, nemoj mi zameriti ako budem malo kasnio sa odgovorom. Pogledaću ako budem imao vremena.
[ Cabo @ 29.07.2009. 16:27 ] @
Da vidimo da li sam ukapirao bar sve ove definicije.
Definicija 1. Polaritet je korelacija (projektivno preslikavanje koje slika projektivni prostor na njemu dualni, npr. tačke na hiperravni), koja je zadana simetričnom matricom  . Polaritet preslikava kolinearne tačke u hiperravni jednog pramena i obrnuto. . Polaritet preslikava kolinearne tačke u hiperravni jednog pramena i obrnuto.Definicija 2. Tačke  i i  (koje ne pripadaju hiperpovrši (koje ne pripadaju hiperpovrši 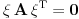 ) su harmonijski konjugovane u odnosu na hiperpovrš ) su harmonijski konjugovane u odnosu na hiperpovrš 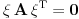 ako je ako je 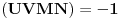 . .Pretpostavljam da je tačka  samokonjugovana ako pripada hiperpovrši? samokonjugovana ako pripada hiperpovrši?Ako je tako, kolinearne samokonjugovane (koje pripadaju hiperpovrši) tačke polariteta se tim polaritetom slikaju na hiperravni nekog pramena, recimo  [što će reći, na primer, da su tangente kroz dve tačke na hiperpovrši paralelne ako je prava kojoj te tačke pripadaju dijametar.] Dalje, svaka takva tačka je presek dve prave koje pripadaju raznim pramenovima, recimo [što će reći, na primer, da su tangente kroz dve tačke na hiperpovrši paralelne ako je prava kojoj te tačke pripadaju dijametar.] Dalje, svaka takva tačka je presek dve prave koje pripadaju raznim pramenovima, recimo  i i  , između kojih je uspostavljeno projektivno preslikavanje (ali, čim to preslikavanje slika pramen na pramen, ono nije korelacija, pa ni polaritet). , između kojih je uspostavljeno projektivno preslikavanje (ali, čim to preslikavanje slika pramen na pramen, ono nije korelacija, pa ni polaritet).Uh... za sad nemam pojma kako dalje? [Ovu poruku je menjao Cabo dana 29.07.2009. u 18:36 GMT+1] [ Nedeljko @ 30.07.2009. 10:50 ] @
Ako polaritet P pridružuje tačkama ravni prave te ravni, onda je tačka A samokonjugovana ako leži na svojoj slici, tj. pravoj P(A).
[ Cabo @ 30.07.2009. 13:28 ] @
Citat: Nedeljko: Ako polaritet P pridružuje tačkama ravni prave te ravni, onda je tačka A samokonjugovana ako leži na svojoj slici, tj. pravoj P(A). Tj. onda je  tangentna hiperravan površi kojoj tačka tangentna hiperravan površi kojoj tačka  pripada. pripada.[ Nedeljko @ 30.07.2009. 19:14 ] @
Da.
[ Nedeljko @ 20.08.2009. 20:06 ] @
Ako ne znaju matematičari, zna wikipedia
http://en.wikipedia.org/wiki/C...ection#Intersecting_two_conics Ovo je rešenje mog problema: elementaran dokaz da dve konike ne mogu imati više od 4 zajedničke tačke. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|