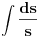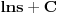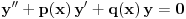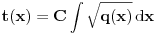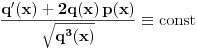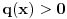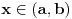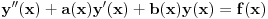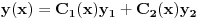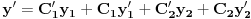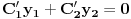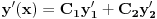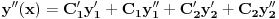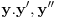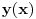C u resenju neodredjenog integrala je neka konstanta kao sto vec verovatno znas. E sad, posto je C konstantan broj onda on moze biti resenje nekog lnC1. E upravo taj lnC1 se pise jer je lakse raditi kada su svi sabirci sa ln. Nemoj da te buni ovo C1( stavio sam ga da bi video da su to dve razlicite konstante), mozes odmah pisati i lnC jer su i C i C1 nepoznate konstante. Dalje obicno resavas tako sto prebacis taj lnC na levu stranu i napises ga u sledecem koraku kao ln(t/C)=ln(s) itd.

Jesi skapirao? Ajd vidi pa mi javni...

skapirao, hvala puno :)

Zdravo svima.Izvinjavam se sto ovo trazim ali, zamolio bih vas da mi pomognete(resite) oko resenja difr. j-ne oblika: y(x)''+k(x)y(x)=0.

Od linearnih DJ na faxu smo resavali DJ sa konstantnim koeficijentima ili sa funkcionalnim koeficijentima (uz to da znamo koja su partikularna resenja). Medjutim za ovu gore ne znam ni jedno partikularno resenje. Jedino sto mi pada na pamet jeste da nekako pogodim jedno partikularno resenje, a potom Liuvilovom formulom da nadjem drugo, pa zatim metodom varijacija konstanti nadjem opste.

Stvarno bih bio zahvalan ako bi mi neko oko ovoga pomogao, i napisao postupak.

Hvala!

Pozdrav!

U zbirci „Diferencijalne jednačine sa elementima teorije“ od Svetlane Janković i Julke Knežević-Miljanović, str. 177, u zadatku 261. je dat mehanizam kako se jednačina smenom svodi na DJ sa konstantnim koeficijentima.

Mora biti ispunjen uslov , a jednačina postaje

Hvala Cabo. Za p(x)=0, q(x) ne moze biti proizvoljna parna funkcija, tako da ne mogu resiti onaj moj problem u opstem slucaju.(dobijem da je q(x)=1/(cx^2)).

Još nešto. Zaboravih da navedem da treba da bude za . I to je uslov za primenu ovog metoda.

Resenje homogenog dela je



Resenje nehomogene jednacine trazimo istoj formi, samo proizvoljne konstante zamenimo proizvoljnim funkcijama





Zahtevamo da je



tj.





I sad izraze za vratis gore u jednacinu. Resenje koje dobijes je opste resenje.