[ Nemanjich @ 31.07.2009. 10:13 ] @
| evo nesto me ovde kopka, mislim da nisam lepo shvatio dokaz al' evo prikacio sam sliku sa onime sto ne znam. Hvala svakome ko pomogne.  |
|
[ Nemanjich @ 31.07.2009. 10:13 ] @
[ Časlav Ilić @ 31.07.2009. 15:30 ] @
Nedoumica ti je rezultat nedovoljno precizne notacije: pošto je skalarni proizvod definicijom vezan za koordinatni sistem (iako se ispostavlja da je invarijantan), tačka između
 i i  u prvom i drugom redu nisu isti operator po preduslovima, već upravo treba dokazati njihovu istovetnost. Zapisano ovako: u prvom i drugom redu nisu isti operator po preduslovima, već upravo treba dokazati njihovu istovetnost. Zapisano ovako: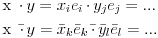 treba pokazati da operatori  i i 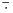 daju isti rezultat. daju isti rezultat.Citat: Nemanjich: [...] Izvinite što je nepregledno, al' ovo je najbolje što mogu. Vidi proguglaj po ključnoj reči „Latex“. Može se koristiti ovde na forumu, kao gore, a može ti poslužiti i profesionalno (npr. na berlinskim univerzitetima se od studenata matematike i informatike već u prvom semestru zahteva da izveštaje rade u latehu). [ Nedeljko @ 31.07.2009. 16:19 ] @
Uvedeš skalarni proizvod preko prvog koordinatnog sistema sa
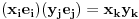 . .Zatim, dokažeš osnovne osobine skalarnog proizvoda (slaganje sa množenjem skalarom i sabiranjem vektora) i onda vektore 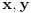 predstavim u drugoj bazi predstavim u drugoj bazi 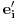 za koju se pretpostavlja da je ortonormirana za koju se pretpostavlja da je ortonormirana 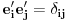 i izračunaš skalarni proizvod. i izračunaš skalarni proizvod.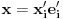 , , 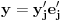 , , 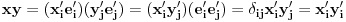 . .Znači, dobio si istu formulu kao da si skalarni proizvod definisao preko druge baze. [ Nemanjich @ 31.07.2009. 17:03 ] @
Hvala i tebi Časlave i tebi Nedeljko.
Ovako, Časlave lepo si mi to pojasnio, ali si mi otvorio jos jedno pitanje(?). Naucio sam linearnu algebru (koliko se trazilo) u okviru mate 2, i u okviru nje skalarni proizvod. Pri definisanju skalarnog proizvoda nigde nismo uzimali u obzir bazu, mislim nismo nigde spominjali vezanost operatora za sistem (mada ipak, nismo ni radili u dva razlicita koordinatna sistema istovremeno). U okviru ovog udzbenika(Analiticka geometrija;Lucic, Rakic, Bokan, Blazic) se takodje nigde ne spominje (ili ja nisam nasao), vezanost operatora za koordinatni sistem. Pa cisto ako imas vremena to malo da mi pojasnis. Nedeljko, mislim da nisam skroz shvatio tvoju ideju. Mislim znam da tu nemas jos mnogo mesta za neko objasnjenje, al' ako mosh ti reci. E, i nisi stavio tacku za skalarni proizvod izmedju x i y (sala mala, nemoj ovo ozbiljno da shvatis :)).Pozdrav. Hvala jos jednom! [ Nedeljko @ 01.08.2009. 09:30 ] @
[ petarm @ 01.08.2009. 13:48 ] @
Citat: Nemanjich: Hvala i tebi Časlave i tebi Nedeljko. Ovako, Časlave lepo si mi to pojasnio, ali si mi otvorio jos jedno pitanje(?). Naucio sam linearnu algebru (koliko se trazilo) u okviru mate 2, i u okviru nje skalarni proizvod. Pri definisanju skalarnog proizvoda nigde nismo uzimali u obzir bazu, mislim nismo nigde spominjali vezanost operatora za sistem (mada ipak, nismo ni radili u dva razlicita koordinatna sistema istovremeno). U okviru ovog udzbenika(Analiticka geometrija;Lucic, Rakic, Bokan, Blazic) se takodje nigde ne spominje (ili ja nisam nasao), vezanost operatora za koordinatni sistem. Pa cisto ako imas vremena to malo da mi pojasnis. Nedeljko, mislim da nisam skroz shvatio tvoju ideju. Mislim znam da tu nemas jos mnogo mesta za neko objasnjenje, al' ako mosh ti reci. E, i nisi stavio tacku za skalarni proizvod izmedju x i y (sala mala, nemoj ovo ozbiljno da shvatis :)).Pozdrav. Hvala jos jednom! Uzmi psa npr. buldoga. Neka je on operator. Drugacije ce se ponasati u dvoristu, na livadi, na izlozbi pasa... a to je jedan te isti pas. Ovo njegovo "delovanje" zavisi od mesta na kom se nalazi i raznih spoljnih uslova. [ Nemanjich @ 01.08.2009. 14:55 ] @
fino i slikovito, samo cini mi se da tu fali neki jasno definisani izomorfizam :). Pozdrav!
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|