Prvo da raščistimo osnovno: Da li ti treba ZAPREMINA (podrazumeva se 3-dimenzionalna) ili N-dimenzionalna zapremina N-dimenzionalne sfere?
Sudeći po integralu, reč je o ovom drugom?

Ne vidim zasto je problem reci zapremina n-dimenzione sfere? Jasno je tacno sta se misli. Za ovo ocito postaje . Nema smisla pricati o trodimenzionoj zapremini n-dimenzione sfere. Ako je n=2 zapremina dvodimenzione sfere mi je ocito povrsina.

Da ali šta je npr.

dx1*dx2*dx3*dx4

ako sfera ima pet dimenzija?

Neka imas neku n-dimenzionu sferu od zlata npr.

Njena zapremina je:

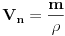
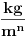
. A to ce biti jednako izrazu koji sam napisao. S tim sto ce gustina biti u drugim dimenzijama. Bice u . To sto si ti napisao nece biti zapremina. Mislim ipak da ne treba odlutati od teme. Jer napisao sam oko cega mi treba pomoc.

Prosto zapremina je proporcionalna dimenziji prostora!

_{[Ovu poruku je menjao petarm dana 01.08.2009. u 01:24 GMT+1]}

Ovde se defakto resava integral u Dekartovim i sfernim koordinatama i izjednacava rezultat. Al zasto bas taj integral? Jel to zato sto je to najlaksi izbor posto znam Poasonov integral? Mislim principijelno ja bih mogao uzeti i neki drugi integral? Zar ne?

Element hiperpovrši.