Nema ogranicenja, zasto bi bilo?

Napisao sam prog za racunanje bilo kog stepena. Medjutim radi bez greske do 10-og stepena. Cim otkucam 11 ispisuje neke gluposti. Nista moracu da cackam jos malo

sve zavisi kako si napisao program. moguce da negde imas nekakvo prekoracenje, pa da zato dobijas pogresne rezultate.

Kod iterativnih metoda je bitan i početni uslov.

Tako je Nedeljko. Npr. nije mi radilo kako treba za odredjeni pocetni uslov a kad sam promenio radilo je ok. Sto se tice prekoracenja sanse su jako male jer sam proverio mnogo puta. Onaj problem sam resio a sad je novi. Sad sve radio ok do neko 25-og stepena i onda kad otkucam neki veci stepen (npr. 30) ispise mi sva ista resenja.

Pa sam ispisivao na ekran nizove i gledao zasto se to desava. Desi se da dok odredjujem clanove uz kvadratnu jednacinu interacijom nema konvergencije nego odlazi u 0. (npr. bude ovako nesto 10,8,4,2,0.1, 0.01, 0.0001.....) odnosno u programu imam deljenje sa ovim pa u jednom trenutnu je deljenje beskonacno (NaN) tako da nekad dobijem i ispis NaN (not a number). Da li su opet u pitanju pocetni uslovi?

Znaci do tog nekog 25-og stepena radi perfektno.

Pa, ako je 0 rešenje...

Možda je bolje da izabereš neku drugu metodu, gde početni uslov nije relevantan. Evo jednog predloga.

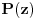
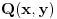
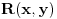
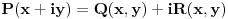
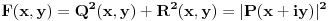
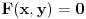
Neka je dat polinom sa kompleksnim koeficijentima. Najpre odrediti polinome i takve da je za sve realne vrednosti x,y, a onda realnu funkciju . Dakle, treba da pronađeš rešenja jednačine . Lako se dokazuje da moduo polinoma ima lokalne minimume u kompleksnoj ravni samo u nulama polinoma, pa možeš koristiti neki gradijentni metod, koji te vodi ka jednom rešenju za bilo koji izbor početnog uslova. Kada nađeš jedno rešenje, onda podeliš polinom sa time i tražiš istom metodom preostala rešenja. No, tako dobijena rešenja treba smatrati samo početnim uslovima za računanje sa nepodeljenim polinomom.

Ne, nije nula resenje...

Pokusacu sa Jenkins-Traub-ovom metodom, samo ako je prvo razumem, a i ovo sto si predlozio nije lose