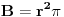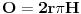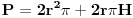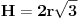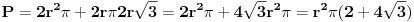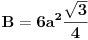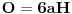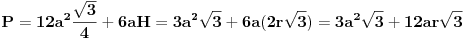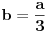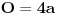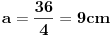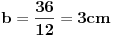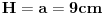[ honijat @ 31.08.2009. 23:35 ] @
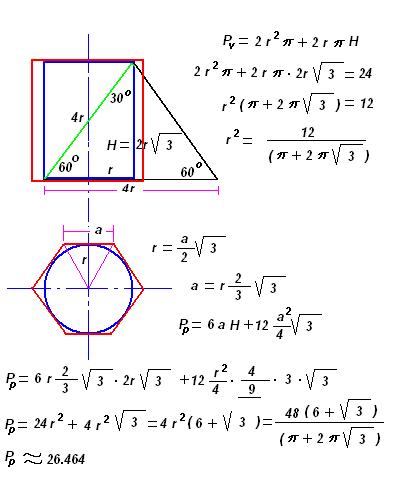
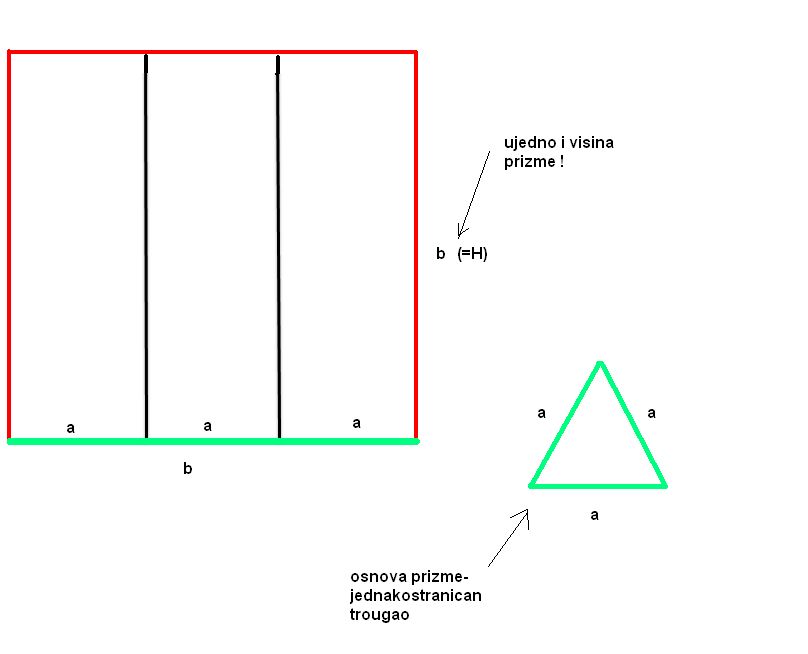
| Posto ja ovo pitane postavljam vec treci put a moderator ga stalno brise jer je procenio da pitanje nije u skladu sa forumom. Ja ne znam koji su to kriterijumi ali evo probat cu još jedanom ali malo sa vise objasnjenja nebili i moderator shvatio da je ovaj zadatak veoma u skladu sa forumom matematika. Daklem radi se o tome da imam samo dva podatka iz kojih ja nisam znao kako da nadjem resenje . Data je pravilna sestostrana prizma u kojoj je upisan valjak cije se baze poklapaju sa bazama prizme . Povrsina valjka iznosi 24 m^2 a dijagonala osnog preseka valjka sa bazom valjka zaklapa ugao od 60 stepeni. Izracunati povrsinu prizme. Molim ljude koji poznaju ovu vrstu zadataka da mi samo ukazu na to dli je ovaj zadatak uz ove podatke uopste moguce resiti i ako jeste kako treba doci bar do jos jednog podatka naprimer : visina ili poluprecnik a ja cu dalje lako. Zahvaljujem se u napred sa nadom da moderator ne proceni da pitanje nije u skladu sa forumom i obrise ga kao predhodna dva !! [Ovu poruku je menjao honijat dana 01.09.2009. u 01:32 GMT+1] |