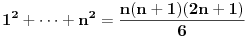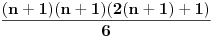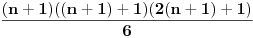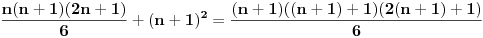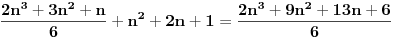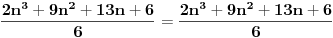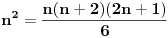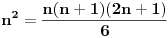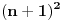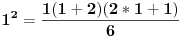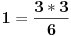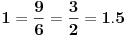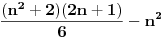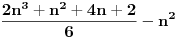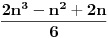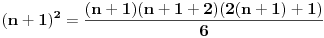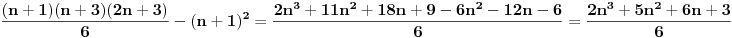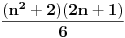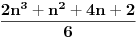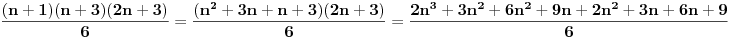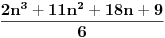[ Andrew91 @ 02.09.2009. 23:01 ] @
| E ljudi, možete postupno da mi rešite ovaj zadatak :D znam da je prost, ali jbg kad ja ne znam ovo novo gradivo, a mi već imamo domaće i sve :S a tek smo drugi dan u školi! Dokazati da za sve prirodne brojeve važi : 1na2+2na2+3na2+...+n na2=n(n+2)(2n+1) (desna strana kroz šest, ne mogu drugačije da napišem zadatak :@ |