[ lepi.cane @ 23.09.2009. 00:52 ] @
|
| Zadatak glasi ovako:
zadatak
E, sad, ja sam nešto kontao da je Lebegova mera od Q jednaka nuli (a ni tog dokaza se ne sećam), pa je dotični integral u stvari jednak 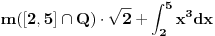
Tu je prvi deo jednak 0 jer je mera od 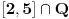 jednaka 0 jednaka 0
[Ovu poruku je menjao lepi.cane dana 23.09.2009. u 02:19 GMT+1] |
[ Nedeljko @ 23.09.2009. 01:03 ] @
[ lepi.cane @ 23.09.2009. 01:09 ] @
Hvala, Nedeljko, odgovorio si mi pre nego što sam se izborio sa tex-om. Dakle to sam i mislio, svodi se na Rimanov integral, jer je skup prekida Lebegove mere 0, ako se dobro sećam.
[ Nedeljko @ 23.09.2009. 10:36 ] @
Gresis.
Funkcija f je prekidna u svim tackama domena. No, ona je jednaka neprekidnoj funkciji x3 skoro svuda na domenu, pa na tom domenu te dve funkcije imaju isti integral.
[ lepi.cane @ 23.09.2009. 18:34 ] @
Jutro je pametnije od večeri. Jasno mi je da je funkcija prekidna u svakoj tački domena (u svakoj okolini bilo koje tačke postoje i racionalne i iracionalne tačke), sem toga da sam pročitao još 20-ak stranica knjige, video bi rešenje. Međutim bilo je već 3 ujutru, a u knjizi nikako da naiđem na rešenje, pa sam pribegao lakšem rešenju - elitesecurity.org. Hvala Nedeljko i izvinjavam se na smetnji.
[Ovu poruku je menjao lepi.cane dana 24.09.2009. u 16:54 GMT+1]
[ lepi.cane @ 24.09.2009. 00:34 ] @
Kad smo već ovde, pokušao sam da dam dokaz da je Lebegova mera skupa racionalnih brojeva nula. Molio bih cenjene posetioce foruma koji su kompetentniji od mene da pogledaju dokaz i ukažu na eventualne greške.

[ Nedeljko @ 24.09.2009. 01:16 ] @
Da, to je opšti dokaz da najviše prebrojivi skupovi mere nula.
[ lepi.cane @ 24.09.2009. 01:22 ] @
Hvala Nedeljko, još jednom. Neke stvari se vrlo brzo sjasne, kad prenoće.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
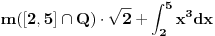
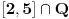 jednaka 0
jednaka 0