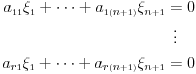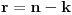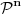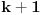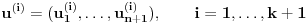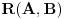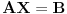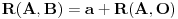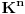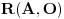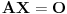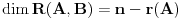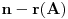[ Cabo @ 24.09.2009. 10:10 ] @
Spremam Nacrtnu (ovog puta usmeni! ), pa sam zapeo kod jedne stvari iz Linearne, kod sistema jednačina.

Naime, u teoriji se kaže sledeće:

Sistem jednačina

ranga određuje -dimenzionu ravan u (u projektivnom prostoru dimenzije ). Kako je vektorski prostor rešenja tog sistema dimenzije , ma kojih linearno nezavisnih vektora prostora rešenja generišu prostor rešenja.

Interesuje me kako je moguće da je prostor rešenja sistema jednačina koji je ranga bude dimenzije ?! Zar ne bi trebalo da bude vektora koji generišu prostor rešenja koji je dimenzije ?!

U teoriji iz Linearne algebre se kaže:

Skup svih rešenja matrične jednačine je i afini potprostor vektorskog prostora , čija je direktrisa prostor svih rešenja odgovarajućeg homogenog sistema . Štaviše, tada je i , jer linearno preslikavanje i njegova matrica imaju isti rang, dok je dimenzija njegovog jezgra .

Kako sada pomiriti teoriju iz Nacrtne geometrije sa teorijom iz Linearne algebre?!
[ Nedeljko @ 24.09.2009. 10:42 ] @
Koliko vidim, linearno nezavisnih resenja ima n+1-r=n+1-(n-k)=k+1, a oni odredjuju k-dimenzionu ravan u n-dimenzionom projektivnom prostoru, zato sto je reprezentacija tacke odredjena do na multiplikativnu konstantu..
[ Cabo @ 24.09.2009. 10:44 ] @
Citat:
Nedeljko: Koliko vidim, linearno nezavisnih resenja ima n+1-r=n+1-(n-k)=k+1,


Zašto , kada je rečeno da je prostor dimenzije ?
[ Nedeljko @ 24.09.2009. 13:46 ] @
Nepoznatih u sistemu ima n+1 i to je sasvim normalno za n-dimenzioni projektivni prostor, jer je vektor koordinata tacke odredjen jednoznacno do na mnozenje nenula skalarom. Dakle, n-dimenzioni projektivni prostor se konstruise u n+1-dimenzionom realnom.