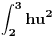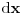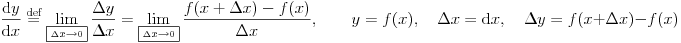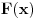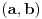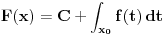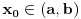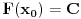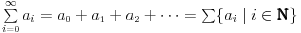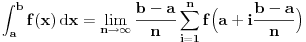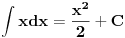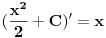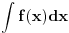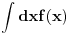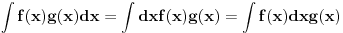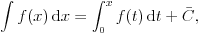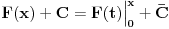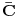|
|
[ Slobica8990 @ 26.09.2009. 02:48 ] @
|
| Da li neko moze da mi objasni sta ono dx pod integralom zaista znaci ( znam da je to diferencijal promenljive) ali sta to meni zaista govori , i kako se dolazi do toga da kad imamo integral treba da se sve podize za 1 stepen , tj. nama su rekli to vam je suprotno od izvoda , samo onako mehanicki da radimo , a mene zanima sta to uopste znaci , i kako su do toga dosli ?!
Hvala |
[ Nedeljko @ 26.09.2009. 07:12 ] @
To je oznaka po kojoj se prmenljivoj integrali. Kako bi inače izračunao 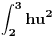 ? [ Cabo @ 29.09.2009. 10:51 ] @
Ovo je vrlo zanimljivo pitanje, i uključuje ono što se retko pominje u organizovanom obliku, bar na beogradskom MATF-u. To je istorija matematike.
U ovom konkretnom slučaju, radi se o oznaci, o simbolu tipa  u koji umesto kvadratića „ubacuješ“ odgovarajuće izraze; u prvi funkciju, a u drugi promenljivu od koje ta funkcija zavisi. Taj simbol predstavlja pokušaj da se odgovori na obrnuto pitanje od pitanja diferenciranja: kako doći do funkcije, ako je poznat njen nagib u određenoj tački?
Kako se došlo do te oznake? To je pitanje istorije matematike. Njutn i Lajbnic su najviše doprineli razvoju integralnog računa i stvaranju takvih oznaka.
Vidi i ovde:
http://en.wikipedia.org/wiki/Integral
http://www.lmgtfy.com/?q=history+of+integrals[ R A V E N @ 29.09.2009. 16:34 ] @
Taj 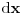 se na primjer u fizici može razumjeti kao beskonačno malen iznos neke veličine. Npr. imaš žicu dužine  i podijeliš je u beskonačno mnogo beskonačno malenih dijelova dužine 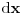 i onda kada vršiš integraljenje, samo sabereš/"pokupiš" te djeliće i dobiješ žicu dužine  .
Ima još na tu temu, zasada ti ne treba više.
Ono "beskonačno malen" i "beskonačno mnogo" su samo apstraktni pojmovi, u realnosti na nekom realnom objektu nikada ne možemo baratati s njima (npr. ne može se ići do beskonačno malene površine neke ploče). [ Cabo @ 29.09.2009. 17:45 ] @
Citat: R A V E N: Taj 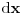 se na primjer u fizici može razumjeti kao beskonačno malen iznos neke veličine.
Ovo je tako zbog definicije izvoda:
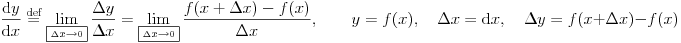 [ Slobica8990 @ 29.09.2009. 21:42 ] @
Ne znam kako da vam postavim pitanje koje me tacno zanima ali pokuascu ponovo
Integral je ANTI DIFERENCIRANJE , znamo vec postupak , tacnije meni nije jasno kako su oni bas do tog postupka dosli , kako su to zakljucili , jel postoji neki dokaz , jer ja na tako nesto nisam naisao u literaturi ( matematika za 4. srednje prirodni smer )
U knjizu su ga samo opisali preko SUME , koji je to princip ( sabiranje beskonacno malih povrsina da se dobija jedna velika naprimer ) , mene ovde zanima taj dokaz.
[ R A V E N @ 29.09.2009. 22:55 ] @
Pitanje je bilo takvo.
Sad pogledah u knjigu i cjelokupni tačni postupak je poprilično dug da se ispisuje ovdje. A u toj tvojoj knjizi mora biti nešto primjereno tvom nivou.
Ako sabiraš površine polja ploče koja je podjeljena na 10 polja dobićeš površinu ploče, a istu površinu ćeš dobiti i ako sabiraš površine polja ploče koja je podijeljena na 1 000 000 polja ili više.
Kod sume operišeš sa sabircima poznatog iznosa, i kada iznos tih sabiraka postane beskonačno malen, a njihov broj beskonačno veliki, onda suma postaje integral.
[Ovu poruku je menjao R A V E N dana 30.09.2009. u 00:17 GMT+1]
[ Cabo @ 30.09.2009. 17:14 ] @
Da, u definiciji figurišu redovi (beskonačne sume, npr. 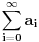 je red), beskonačno male funkcije itd. Ne znam da li se to radi u srednjoj. [ Nedeljko @ 02.10.2009. 23:28 ] @
Citat: Slobica8990: Integral je ANTI DIFERENCIRANJE , znamo vec postupak , tacnije meni nije jasno kako su oni bas do tog postupka dosli , kako su to zakljucili , jel postoji neki dokaz , jer ja na tako nesto nisam naisao u literaturi ( matematika za 4. srednje prirodni smer ).
Neodređeni integral neke funkcije na nekom intervalu je po definiciji skuppp svih primitivnih funkcija te funkcije na tom intervalu.
Određeni integral nije funkcija, nego konstanta, koji se definiše kao granična vrednost Rimanovih suma te funkcije kada finoća podele teži nuli.
Određeni i neodređeni integral povezani su na primer Njutn-Lajbnicovom teoremom. Ta formula već ima dokaz. Takođe, primitivna funkcija 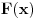 neprekidne funkcije  definisane na intervalu 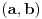 ima oblik
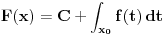 ,
gde je 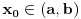 , a  bilo koja konstanta (zapravo, važiće 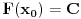 ). Ovo je takođe teorema.
Dokazi osnovnih stavova uvek zavise od izbora definicija/aksioma. [ Nedeljko @ 02.10.2009. 23:30 ] @
Citat: Cabo: Da, u definiciji figurišu redovi (beskonačne sume, npr. 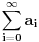 je red), beskonačno male funkcije itd. Ne znam da li se to radi u srednjoj.
U definiciji učestvuju isključivo konačne sume, a klasična analiza ne poznaje ni beskonačno male ni beskonačno velike veličine. [ Cabo @ 03.10.2009. 17:27 ] @
Citat: Nedeljko: U definiciji učestvuju isključivo konačne sume, a klasična analiza ne poznaje ni beskonačno male ni beskonačno velike veličine.
Netačno, izraz je sa beskonačno mnogo članova, 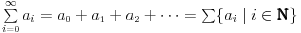 , zato što skup prirodnih brojeva ima kardinalni broj  . Rezultat tog izraza je ili realan broj ili se ne definiše.
[Ovu poruku je menjao Cabo dana 03.10.2009. u 18:56 GMT+1][ Nedeljko @ 03.10.2009. 19:16 ] @
U definiciji integrala se ne pominju nikakve beskonačne sume. Rimanove sume i gornje i donje Darbuove sume su konačne sume (po konačnim podelama). Takođe, u definiciji Lebegovog integrala se takođe koriste konačne sume. Ponovi definicije.
[ Cabo @ 03.10.2009. 19:33 ] @
Možda sam nepažljivo upotrebio reč „definicija“ (a i davno sam položio Analizu 2).
Ipak, važi sledeće:
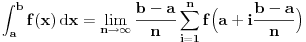 DODATAK:
DODATAK:
Da, integral se definiše vrlo izokola, preko maksimuma i minimuma funkcije. Dužine segmenata se sve više smanjuju, i teže ka nuli, a istovremeno njihov broj raste u beskonačnost. Nije baš-baš red, ali liči...
Sludele me geometrije i pedagogije.  Odavno nisam radio neki analitički predmet.
[Ovu poruku je menjao Cabo dana 03.10.2009. u 21:01 GMT+1][ Nedeljko @ 03.10.2009. 20:07 ] @
Tako je. To je limes po konačnim sumama, kojima broj sabiraka teži beskonačnosti.
[ petarm @ 03.10.2009. 20:55 ] @
Mislim da je Slobica8990 hteo da pita sledece. Odakle vi znate da je
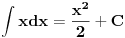
Odnosno da li je to utvrdjivano po principu 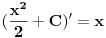 pa je tako formirana tablica koju danas koristimo. To je bilo njegovo pitanje kolko sam ja shvatio.
Ja bih hteo samo reci nesto na sta je Cabo skrenuo paznju, ako se ne varam, na sledeci redosled u zapisu
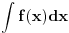
Fizicari cak vrlo cesto napisu i
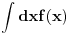
Hocu reci taj redosled i nije bitan. Sta vise
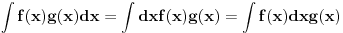
Nije problem ni ovako napisati ako razumemo sta racunamo! [ Nedeljko @ 03.10.2009. 21:33 ] @
To što se tiče pisanja je OK.
Da, neodređeni integral funkcije definisane na intervalu je definisan kao skup svih primitivnih funkcija te funkcije na tom intervalu, pa su osobine neodređenog integrala posledice osobina izvoda.
[ Cabo @ 04.10.2009. 16:05 ] @
Još nešto. Istorijski su prvo nastali određeni integrali, pa tek onda neodređeni.
Takođe, neodređeni integral se može definisati preko određenog sa promenljivom granicom:
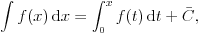
jer je 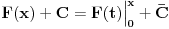 .
IZMENA: Pretvorio sam ono  u 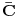 , da ne bi bilo zabune. Tu se u stvari radi o „ 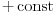 “.
[Ovu poruku je menjao Cabo dana 04.10.2009. u 20:06 GMT+1]
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|