[ honijat @ 27.09.2009. 13:51 ] @
|
| Ja imam jedan problem pri resavanju trigonometrijskih jednacina i recimo dobije se rezultat na pr :
x=pi/3+2kpi ili x=pi/4+kpi i slicno nije mi potpuno jasno sta predstavlja koeficient k.
Ako ima neko raspolozen da mi precizno objasni sta bukvalno predstavlja koeficient k ? |
[ enter08 @ 27.09.2009. 14:02 ] @
Ako se ne varam to mozes zakljuciti posmatrajuci trigonometrijski krug. 2kpi znaci ce ugao biti uvijek djeljiv sa 90... Tj. za svako k 2kpi ce imati vrijednost 1 ili -1. I vrijednost cosinusa ce uvijek biti 0 s obzirom da je cos projekcija na x osu. Davno sam ovo ucio... Ne sjecam se vise.
[ marko1981 @ 27.09.2009. 15:06 ] @
Uz rešenje
x=pi/3+2kpi
treba napisati za koje vrednosti k važi rešenje. K uglavnom pripada celom skupu celih brojeva (..., -2, -1, 0, -1, -2, ...).
To znači da rešenja ima bezbroj, odnosno da svaki broj x od sledećih, predstavlja rešenje jednačine:
...
x = pi/3 + 2*(-1)*pi = -5pi/3,
x = pi/3 + 2*0*pi = pi/3,
x = pi/3 + 2*1*pi = 7pi/3
...
A uzrok je periodicnost trigonometrijskih funkcija sa periodom 2pi, odnosno zbog toga što je:
sin(-5pi/3) = sin(pi/3) = sin(7pi/3) = ...
Naravno, da bi ovo shvatio, moraš i da razumeš trigonometrijski krug, kao što je napisao enter08.
Slično, rešenje jednačine sinx = 0 bi bilo
x = kpi, k e Z
jer je (sad ću napisati u stepenima, a ne u radijanima)
sin 0 = sin 180 = sin 360 = sin 540 = ... = 0
[ honijat @ 27.09.2009. 20:09 ] @
Ma slazem se ja sa svim tim i mislim da dobro razumem trigonometrijsku kruznicu . Ali koji su to uslovi zadatka kada ja mogu ili moram da uvrstim umesto k neki ceo broj i ako to uradim dali je u tom momentu tacno definisan ugao i nema mogucnosti za druga resenj.
[Ovu poruku je menjao honijat dana 28.09.2009. u 13:15 GMT+1]
[ EArthquake @ 27.09.2009. 21:35 ] @
pa ne moras uvek da preciziras koje je k tacno , samo stavis k pripada Z (k e Z :) )
sto oznacava da je skup resenja beskonacan , posto je sin/cos periodicna funkcija , kako su vec rekli ljudi u prethodnoh poruci
a obicno , kad ti treba konkretan ugao , uzimas k=0 ,
ili , ako ti je bas u datom zadatku iz nekog razloga lakse , neko drugo k
uslov zadatka recimo moze biti da ti se resenje nalazi izmedju 0 i 2pi
ili tako nesto , sto ti ogranicava interval
recimo , ako ti po uslovu zadatka resenje lezi u prvom kvadrantu
a ti dobijes resenje kao
pi/3 + 2*k*pi , onda uzimas samo pi/3 kao resenje
[ honijat @ 27.09.2009. 23:10 ] @
Pa i ne mislim ja da uvek treba precizirati ali predpostavimo da mi nesto ogranicava,neki vanredan slucaj na primer : imamo proizvodnju spiralnih opruga i da masini treba zadati uslov iz kog ugla pocinje da se savija zica i gde treba da bude kraj zici , i da to zapisemo ovako pocinje da savija iz pi/3 i da odseca zicu na 1080 stepeni od pocetne tacke. Alida to ne pisemo tako nego jednostavno pi/3+2*pi*3 ==> pi/3+6*pi . I koji je to uslov koji mi govori kada pisem 2*k*pi a kada k*pi ?
[Ovu poruku je menjao honijat dana 28.09.2009. u 13:36 GMT+1]
[ zzzz @ 28.09.2009. 17:39 ] @
Citat: honijat: . I koji je to uslov koji mi govori kada pisem 2*k*pi a kada k*pi ?
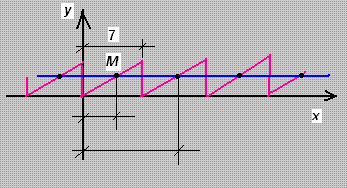
Na donjoj slici imaš periodičnu funkciju (crveno) sa periodom sedam.
I našao si presječnu tačku M sa onim plavim pravcem.Ali to nije jedino rješenje jer imamo još tih presjeka.
Neka je osnovno rješenje x(0)=4.Pokušaj napisati i sva ostala rješenja.
(Nije lijepo da pišeš nešto ovako:-3,4,11,18,...)
 [ zzzz @ 28.09.2009. 23:43 ] @
Citat: honijat: I koji je to uslov koji mi govori kada pisem 2*k*pi a kada k*pi ?
Još malo pomoći.Ako znamo pravilo komutacije (3*5=5*3) onda ovu
gornju misteriju možemo napisati ovako:
I koji je to uslov koji mi govori kada pisem k*(2*pi) a kada k*(pi) ?
(A kada k*7,rekoh ja!)[ honijat @ 29.09.2009. 16:56 ] @
Sta zakon komutacije ima veze sa uslovom da pri pisanju resenja trig jednacine dodam ono 2*p*k ili samp pi*k. Mene zanima koji uslov zadatka mi govori da resenju zadatka naprimer pi/3 treba dodati 2*pi*k a zasto ne pi*k jer se u 2*pi nalazi i pi i ako je k tu samo zato da nam kaze da se resenje nalazi do beskonacno posle svakog perioda a nikad nemamo potrebu da ga zamenimo sa nekim celim brojem pa cemu onda to pisati i uvek naznaciti da k moze biti bilo koji ceo broj i pozitivan i negativan do u beskonacno?
[ zzzz @ 29.09.2009. 17:56 ] @
Pročitaj pažljivo ponovo pa ćeš shvatiti.
A onda ćeš znati da za rješenje nekih trig. jednadžbi netrebaš nikakvo
prokleto k,a ni 2k.Naprimjer za 2x+sinx=1.
[ honijat @ 29.09.2009. 19:13 ] @
Neznam mozda me i ne razumes .Kod resenja pi/3+2*pi*k samo pi/3 je resenje a ovaj dodatak govori da se resenje nalazi posle svakog perioda u tacki pi/3 i to moramo da naznacimo da je to bezbroj ili k puta i da brojevi moraju biti celi i u minus i u plus . Pa cemu to kad je to bukvalno aksioma. I dali mozes malo jasnije da mi objasnis kako da znam kad treba pisati 2*pi a kada samo pi ostavimo po strani jednacine kojima to uopste ne treba.
[Ovu poruku je menjao honijat dana 29.09.2009. u 22:38 GMT+1]
[ zzzz @ 29.09.2009. 21:50 ] @
kako da znam kad treba pisati 2*pi a kada samo pi
(kao da si nešto žestoko preskočio)
Trebaš znati koliki je period funkcije koju rješavaš.Najbolje da je skiciraš.Pa ako je period pi pišeš k*pi.Ako je 2pi piši 2kpi.Ako je 3pi piši 3kpi.Ako je 7
piši k*7.
Za periodičke funkcije vrijedi f(x)=f(x+P)=f(x+k*P). P je period.
Za funkciju y=sinx; P=2pi
Za funkciju y=tgx; P=pi
Za funkciju y=cos^2x; P=pi
Za funkciju y=cos4x; P=pi/2
Za funkciju y=ctg(pi/7(x)) P=7
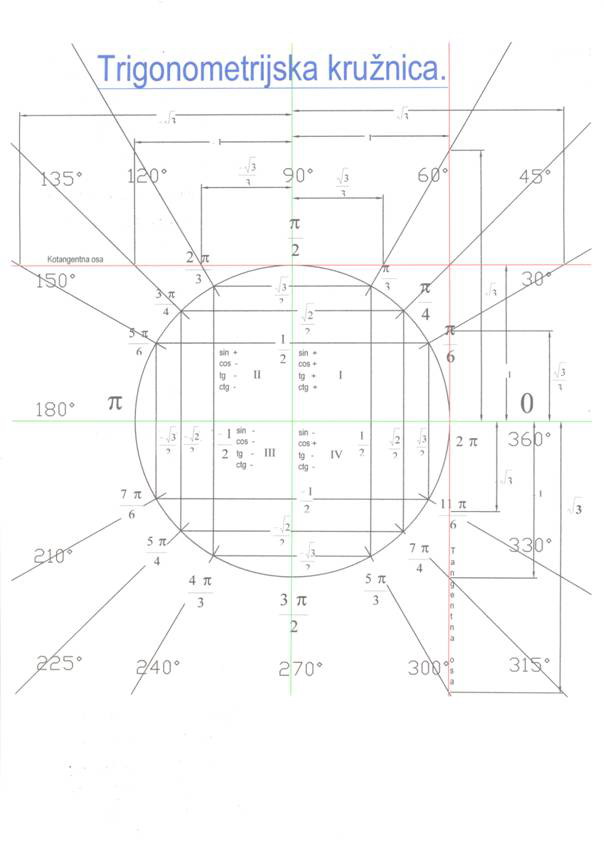
Nacrtaj sam trig.krug pa se uvjeri.
[ honijat @ 29.09.2009. 22:20 ] @
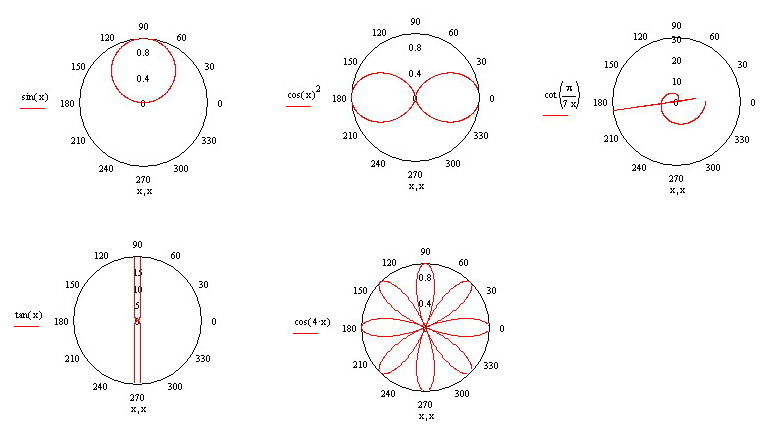
Evo kruznice a evo svake slike posebno pa ako imas strpljenja da mi objasnis kako sa slike mogu zakljuciti da ima ovaku ili onaku periodu
[Ovu poruku je menjao honijat dana 30.09.2009. u 14:04 GMT+1]
 [ Cabo @ 30.09.2009. 17:02 ] @
Prosto objašnjenje, da prostije ne može biti:
Ako imaš neki faktor  kojim se množi argument trigonometrijske funkcije  , dakle 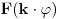 , onda se njen period deli tim faktorom. Na primer:
Funkcija 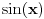 ima period  .
Funkcija 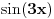 ima period 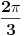 .
Funkcija 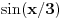 ima period 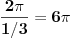 .
Uopšte, funkcija 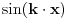 ima period 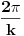 .
I što se zbunjuješ polarnim graficima kada je daleko lakše gledati „obične“ grafike trigonometrijskih funkcija, i periodi se daleko lakše uočavaju?
IZMENA: Sad sam malo bolje pročitao prve poruke. Izgleda da ti nije jasno šta je uopšte period funkcije. To je realni broj za koji funkcija, kada joj se argument sabere sa njim, ima istu vrednost kao i za početnu vrednost argumenta. Dakle, ako je  period funkcije  , onda mora da važi: 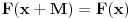 . To znači da će funkcija imati istu vrednost i za svako 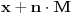 koje pripada domenu, u idealnom slučaju za sve 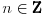 .
To da li se domen periodične funkcije zadaje sa ili bez „ 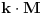 “, perioda, zavisi od uslova zadatka. Na primer, ako je eksplicitno rečeno da se funkcija 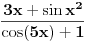 posmatra na segmentu 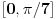 , onda ne dodaješ  „puta nešto“.
[Ovu poruku je menjao Cabo dana 30.09.2009. u 20:19 GMT+1][ honijat @ 30.09.2009. 20:17 ] @
Cabo hvala na komentaru ali sad oped imam nedoumicu. Ja mislim da je perioda deo ugla ili nekakav ugao a da koeficient k govori koliko puta ga moze biti do u beskonacno ili u minus ili u plus.
[Ovu poruku je menjao honijat dana 30.09.2009. u 21:28 GMT+1]
[ Cabo @ 30.09.2009. 20:33 ] @
Neka je 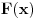 periodična sa periodom  .
Dakle, 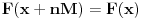 za 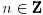 .
Uzmimo da posmatramo funkciju kojoj je argument pomnožen nekim faktorom  :
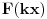 . Njoj je period 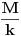 . Funkcija nema zadan poseban domen, pa možemo da množimo sa 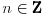 koliko nam drago, drugim rečima možemo da sabiramo argument sa 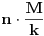 .
Neka je 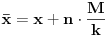 . Imamo: 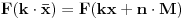 . Šta imamo gore? 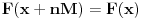 za 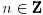 . Dakle, dobićemo 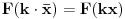 . To smo i hteli da dobijemo. [ honijat @ 30.09.2009. 21:04 ] @
Ok kazes :Neka je F(x) periodicna sa M. moj problem i jeste kako da odredim vrednost za M.
[ RMAN @ 01.10.2009. 01:41 ] @
Pa gledas u funkciju i razmisljas koji broj da stavis umesto  da bi dobio istu vrednost funkcije.
Na primer imas 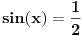 i koja su resenja za x?
Kada je sinus jednak 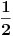 ? Jednak je za 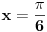 ILI za 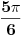 .
Ali nisu samo ovo resenja, ako na ova resenja dodas 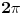 , 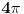 , 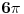 , 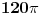 opet ces doci na isti ugao sto znaci da je i ovo resenje.
Znaci resenja za x su 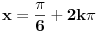 za svako 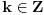 ili 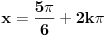 za svako 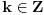 [Ovu poruku je menjao RMAN dana 01.10.2009. u 02:56 GMT+1]
[Ovu poruku je menjao RMAN dana 01.10.2009. u 09:42 GMT+1]
[Ovu poruku je menjao RMAN dana 01.10.2009. u 02:56 GMT+1]
[Ovu poruku je menjao RMAN dana 01.10.2009. u 09:42 GMT+1][ miki069 @ 01.10.2009. 08:10 ] @
Mnogo je 11*pi/6.
Jednačina sin(x) = a gde je -1<=a<=+1 ima rešenja:
x=(alfa) + 2*k*pi i
x=(pi-alfa) + 2*k*pi
gde je alfa=arcsin(a)
Primer:
sin(x) = 1/2
ima rešenja:
x=pi/6+2*k*pi i
x=5*pi/6 +2*k*pi
alfa=arcsin(a) je osnovna vrednost alfe od -pi/2 do +pi/2 i treba je gledati sa trigonometrijskog kruga
[ RMAN @ 01.10.2009. 08:41 ] @
Uh moja greska  . Ja sam 180 stepeni posmatrao kao 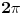 .
Eto sta se desava kad razmisljas u 3 ujutru 
Ispravljeno je..... [ zzzz @ 01.10.2009. 10:06 ] @
Čovjek shvata da su trig.funkcije periodičke i da vrijedi:
trig.f(x)=trig.f(x+M)=trig.f(x+2M)=trig.f(x+3M)=......
ali ne zna kako doći do ovog M za konkretnu funkciju.
Primjetio je da se nekad koristi pi,a nekad 2pi.Sad smo
dodali još kojekakvih mogućnosti.Trebao bi rasčistiti šta je
to lučna mjera ugla,veza stepeni i radijana,definicija osnovnih trig.funkcija na trokutu i trig.kružnici,grafove funkcija,koordinatni sistemi i još ko zna šta.
[ Cabo @ 01.10.2009. 18:04 ] @
@honijat:
Rekoh da gledaš grafik. E sad, po mom skromnom mišljenju, najlakše je gledati običan grafik trigonometrijskih funkcija, gde vidiš da „talas“ koji, na primer, pravi sinusoida mora jednom da se vrati na istu visinu i da počneš da crtaš jedan deo te sinusoide koji si već crtao. Lepo se vidi da je razmak od prvog crtanja do drugog  .
Ako pitaš za neki formalni način kako doći do perioda, verovatno bi moglo nešto da se iskombinuje preko Tejlorovog razvoja, slično Numeričkoj matematici, ali je po meni to bespredmetno, osim ako ne pišeš doktorsku disertaciju. Za sve svakodnevne potrebe, nacrtaš na brzinu skicu funkcije i vidiš koliko ti treba da ponavljaš crtanje talasa. To je to. A mogao bi i da nabubaš (što da ne?) činjenicu da je period sinusa  . :-S
Dokazati da je  period funkcije  je lako ako nabodeš pravu vrednost. Pošto znaš da važi jednakost 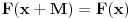 za jedno  i sve  iz domena, samo primeniš indukciju na sledeći način: 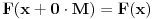 (trivijalno), 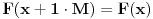 , 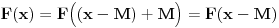 , 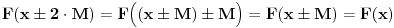 (baza indukcije), 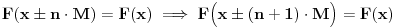 . Lako se dokazuje.
[Ovu poruku je menjao Cabo dana 01.10.2009. u 19:44 GMT+1][ honijat @ 05.10.2009. 11:51 ] @
LJudi bas ste se potrudili da ovo dobro objasnite i zzzz je dobro primetio da ja imam problem da sa sigurnoscu odredim dali funkcija ima osnovni period period od pi ili 2pi ili neki n*pi. Mada je malo lose zakljucio da treba da rascistim sa nekim osnovnim stvarima iz trigonometrije jer da toga nema ne bi moglo postojati interesovanje na ovakav nacin ali to je sigurno zbog toga sto uporno postavljam jedno te isto pitanje ali na drugi nacin a to je zato sto vase dobre poznavanje ove problematike to i sprecava da to iskazete na vrlo prost nacin razumljiv i za onog ko bas nije sa svim stvarima nacisto. Ovo radim jer ova problematika nije nigde u udzbenicima dobro objasnjena procito sam negde komentar jednog profesora da je to zbog toga sto se u srednjoj skoli na prvon kursu iz trigonometrije izucavaju takve funkcije za koje ovo bas i nije toliko potrevbno a u drugom kursu se ocekuje da to ucenici vec znaju i taku nastaje taj problem kod vecine onih kojima to nije sa svim jasno. I mene je to navelo da ovo pitam vas pa bi vas zamolio da za dveili tri funkcije od kojih jedna ima period 2*pi a druge neki n*pi i da tu racunicu vrlo postuono napravite ovde verujt mi da ce ovo mnogima pomoci da do kraja shvate ovu problematiku samo se stide da to javno kazu a neki cak i neznaju sta neznaju.
Unapred hvala!!
[ Cabo @ 05.10.2009. 11:54 ] @
Citat: honijat: za dveili tri funkcije od kojih jedna ima period 2*pi a druge neki n*pi i da tu racunicu vrlo postuono napravite ovde
Nisam siguran da sam shvatio šta je ovde pitanje/problem. o_O [ miki069 @ 05.10.2009. 13:18 ] @
Aj kad niko ne čita ja ponovo pišem citat iz Veneove zbirke za srednju školu:
"Jednačina sin(x) = a gde je -1<=a<=+1 ima rešenja:
x=(alfa) + 2*k*pi i
x=(pi-alfa) + 2*k*pi
gde je alfa=arcsin(a)" kraj citata.
alfa=arcsin(a) je osnovna vrednost alfe od -pi/2 do +pi/2 i treba je gledati sa trigonometrijskog kruga
Prostije od ovoga ne može. U istoj zbirci ima i za jednačine cos(x)=a, tg(x)=a i ctg(x)=a.
Primer 1:
sin(x) = 1/2
ima rešenja:
x=pi/6+2*k*pi i
x=5*pi/6 +2*k*pi
što se ne može objeniti u jednozačan zapis i ostaju 2 posebne grane rešenja.
Primer 2:
sin(x) = 1
ima rešenja:
x=pi/2+2*k*pi i
x=pi/2 +2*k*pi
što se može objediniti u jednu granu rešenja x=pi/2+2*k*pi jer je isto rešenje.
Primer 3:
sin(x) = 0
ima rešenja:
x=0+2*k*pi i
x=pi +2*k*pi
što se može objediniti u jednu granu rešenja x=k*pi i stvara lažnu sliku da je period pi a ne 2*pi.
Sin(x) ima period 2*pi, nego tebe izgleda zezaju 2 stvari:
- objedinjavanje rezultata kao u Primeru 3. i
- kada u igri nije sin(x) već sin(2*x), sin(3*x), sin(x/4)... to je već Cabo objasnio da umesto x menjaš taj novi ugao i onda rešiš x. Time se i period za sin(w*x) menja u (2*pi)/w kako je Cabo lepo i objasnio a Milan skicirao.
[Ovu poruku je menjao miki069 dana 05.10.2009. u 14:36 GMT+1]
[ honijat @ 05.10.2009. 14:18 ] @
Cabo mislio sam da uzmes jedan zadatak kao da si na casu i imas pismeni zadatak i da ga odradis.Ali dobro ima tu sad dosta materijala u vezi sa koeficientom k da vas ne gnjavim vise imam drugo pitanje : Ako je poznat sinus dali mozemo odrediti za koji je to ugao, naravno bez kalkulatora?
[Ovu poruku je menjao honijat dana 05.10.2009. u 16:14 GMT+1]
[ honijat @ 06.10.2009. 17:58 ] @
Nije valjda da niko nezna kako to programeri isprogramiraju kalkulator?
[ Cabo @ 06.10.2009. 18:16 ] @
Citat: honijat: Cabo mislio sam da uzmes jedan zadatak kao da si na casu i imas pismeni zadatak i da ga odradis.Ali dobro ima tu sad dosta materijala u vezi sa koeficientom k da vas ne gnjavim vise imam drugo pitanje : Ako je poznat sinus dali mozemo odrediti za koji je to ugao, naravno bez kalkulatora?
[Ovu poruku je menjao honijat dana 05.10.2009. u 16:14 GMT+1]
Ovo pitanje je slično pitanju određivanja perioda neke funkcije. Slično se i rešava:
1. Nađi vrednost u tablici (ili je nabubaj).
2. Skiciraj grafik (običan ili jedinični krug) i sa njega zaključi o kom uglu se radi.
[ honijat @ 06.10.2009. 20:36 ] @
Mislio sam na numericko odredjivanje kao ono preko Tejlorovih aproksimacija ili Maklorenovih? Astose tice toga da nabubam tu nema problema ali ja bi to da shvatim.Naravno ako je moguce.
[Ovu poruku je menjao honijat dana 07.10.2009. u 00:28 GMT+1]
[ miki069 @ 07.10.2009. 09:42 ] @
sin(alfa)=X za -1<=X<=1
alfa = arcsin(X) koja je neprekidna i više puta diferencijabilna za X=0 i onda arcsin(X) razviješ u Mekloranov (Tejlorov za X=0)po obrascu
f(X) priblizno = f(0) + f'(0)*X/(1!) + f"(0)*X^2/(2!) + f"'(0)*X^3/(3!) +... do željene tačnosti
[ Nedeljko @ 07.10.2009. 10:44 ] @
Period resenja zadatka se ne moze odrediti bez postavke zadatka.
Dajte zadatak, pa da vidimo.
[ honijat @ 07.10.2009. 13:44 ] @
miki069
sin(alfa)=X za -1<=X<=1
alfa = arcsin(X) koja je neprekidna i više puta diferencijabilna za X=0 i onda arcsin(X) razviješ u Mekloranov (Tejlorov za X=0)po obrascu
f(X) priblizno = f(0) + f'(0)*X/(1!) + f"(0)*X^2/(2!) + f"'(0)*X^3/(3!) +... do željene tačnosti
Ovo sve ce za resenje dati vrednost arcsin iz datog ugla ali ja se pitam dali moze obratno ako ti je poznat arcsin pa iz njega da dobijemo koji je to ugao i ne samo arcsin vec oiz drugih trig funkcija?
[ honijat @ 07.10.2009. 14:07 ] @
Nedeljko uzmi jedan primer tebi poznat na kome naj lakse mozes objasniti ovo pitanje, ja ovo u globalu uvek odradim ali nikad nisam sto % siguran da funkcija ima period od 2*pi ili samo pi ili neko n*pi .
Period resenja zadatka se ne moze odrediti bez postavke zadatka.
Dajte zadatak, pa da vidimo.[/quote][quote] Nedeljko:
[ Nedeljko @ 08.10.2009. 11:09 ] @
Pa, daj ti zadatak koji ne umeš da rešiš, kao polaznu tačku.
[ honijat @ 08.10.2009. 12:16 ] @
Nemam ja problem da resim zadatak ali kad ga resim i dobijem resenje naprimer 2pi/3 uzto treba da napisem +2pi*k ali ja to uradim vise zato sto znam napamet neke stvari ali ja nisam siguran da je to bas tako pa pokusavam cuti kako su to naucili neki drugi ljudi .Dalise period odredjuje iz resenja ili iz jednacine koju dobijem za resavanje .Recimo ako imamo zadatak kao u prilogu sta iz ovog zadatka meni govori da da se ovde resenje nalazi posle svako 2*pi?
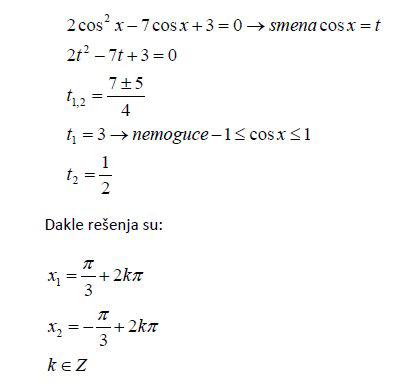 [ zzzz @ 08.10.2009. 13:35 ] @
Citat: honijat: miki069
sin(alfa)=X za -1<=X<=1
alfa = arcsin(X) koja je neprekidna i više puta diferencijabilna za X=0 i onda arcsin(X) razviješ u Mekloranov (Tejlorov za X=0)po obrascu
f(X) priblizno = f(0) + f'(0)*X/(1!) + f"(0)*X^2/(2!) + f"'(0)*X^3/(3!) +... do željene tačnosti
Ovo sve ce za resenje dati vrednost arcsin iz datog ugla ali ja se pitam dali moze obratno ako ti je poznat arcsin pa iz njega da dobijemo koji je to ugao i ne samo arcsin vec oiz drugih trig funkcija? (pretpostaviću da si se zapetljao želeći
pitati kako se izračuna ugao iz poznate vrijednosti sinusa.)
Razvoj u tejlorov red već nakon nekoliko članova daje visoku tačnost.
Tako radi kalkulator,a tako su nekad izrađivane tablice pješke.Probaj!
Evo za ovaj tvoj zadatak napravio sam skicu rješenja.
Kad nekoliko puta rješiš uz pomoć skice kasnije ti neće trebati.
Primjetićeš da za sin(x)=a kao i cos(x)=b imamo uvijek dva osnovna
rješenja za x,a period je 2pi.Kad rješavaš tg i ctg stvari stoje malo drukčije.Prouči to.
Pazi još i na ovo: sin(m/n*x)=a, pa nađemo rješenje za m/n*x=R.
Period od 2pi vrijedi za ovo R,a ne za x.Za konačno
rješenje x=R*n/m pokušaj sam pronaći period.
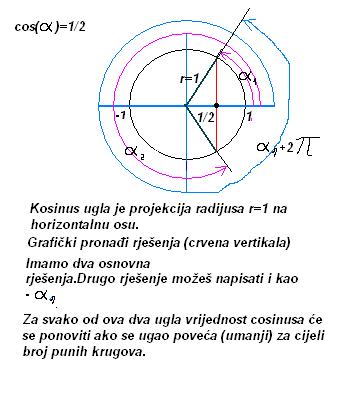 [ honijat @ 08.10.2009. 16:02 ] @
ZZZZ u pravu si vec sam se sav spetljao ,ova skica je menipotpuno jasna ali svaki ugao ce se ponoviti za (taj ugao + 2*pi ) i sta je razlog da se nekima dodaje 2*pi anekima n*pi gde n moze biti ivece i manje od 2. Ajde razvij mi molim te neku vrednost sin ili cos u red da i da dobijes ugao za taj sin ili cos .
[ Nedeljko @ 08.10.2009. 17:08 ] @
Kosinus je  periodilna funkcija. On je u intervalu širine  jednak vrednosti 1/2 u tačno dve tačke itd. [ zzzz @ 08.10.2009. 18:40 ] @
Citat: honijat: ...,ova skica je menipotpuno jasna ali svaki ugao ce se ponoviti za (taj ugao + 2*pi ) i sta je razlog da se nekima dodaje 2*pi anekima n*pi gde n moze biti ivece i manje od 2. Ajde razvij mi molim te neku vrednost sin ili cos u red da i da dobijes ugao za taj sin ili cos .
Ajde prevedi šta si htio reći.Zar nisi shvatio iz skice koliki je P za onaj
tvoj zadatak?Zanima li tebe uopšte koliki je P i zašto ti treba?
"ali svaki ugao ce se ponoviti za (taj ugao + 2*pi )"
Ne, nego vrijednost kosinusa će biti ista ako se osnovnom rješenju
doda ili oduzme proizvoljan broj perioda.Ugao od 420° je sedam puta veći od 60°,ali kosinusi su im isti.Period je 2pi (360°,puni krug).
Dakle X=pi/3+n* 2pi.Ili X=60° +n*360°.Ili 60°+k*puni krug.
Imamo rješenja 60°,420°,780° itd kao i -300,-660 itd.
A iz drugog rješenja X=5pi/3+n* 2pi imamo: -60°,300°,660° itd.
Zašto ovdje ne napišemo n*1pi?Dodaj na onom
crtežu prvom rješenju 180 stepeni i imaš kosinus takvog ugla negativan,
-1/2.To nije rješenje jer mi tražimo za koje uglove je cosinus jednak 1/2.
Da li ovo možeš shvatiti?
A zašto onda puni krug nije period za sve funkcije nego je to nekad samo
pola kruga?(P=pi)
Probaj riješiti funkciju tg(x)=1. X=45°+n*P.Nacrtaj trig. krug i nađi period.Vidjećeš da je i tg(225°)=1.U trećem kvadrantu sinus i kosinus
su negativni pa je tangens pozitivan.
http://www.pmf.untz.ba/studijs...es/AlmiraHasakovic-prosper.pdf
http://www.holo.hr/Formule/Pre.../M34/fid/Mat30-01/Default.aspx
http://www.math.uniri.hr/~ddumicic/file/trigonometrijske_MZI1.pdf
Ovdje imaš način računanja vrijednosti trig.funkcija:
http://www.dodaj.rs/f/3W/N4/358pZ3lq/tejlor-maturski.pdf
Samo ne znam šta će ti ovo i zašto trčiš pred rudu. [ honijat @ 08.10.2009. 23:11 ] @
Upravu ste nisam misli da cu se ovako zapetljati ali tako radeci sa kalkulatorom pa rekoh to su ljudi to jest programeri isprogramirali verovatno postoji neka formula po kojoj to procesor radi i tako postavih pitanje i evo tu sam gde sam izvinjavam se ako sam koga namucio i ako mi neke od ovih stvari i dalje nisu ciste ipak mnogo drugacije vidim sve ovo posle ovih postova.
Hvavala svima !!!
[Ovu poruku je menjao honijat dana 09.10.2009. u 22:03 GMT+1]
[ Nedeljko @ 08.10.2009. 23:22 ] @
Pa, ako rešavaš jenačinu  , onda je 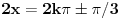 , odnosno,  . Eto ti slučaja kada sa kosinusom imaš period skupa rešenja jednak  . [ miki069 @ 09.10.2009. 01:40 ] @
Ako rešavaš jednačinu:
cos(X) = 0 onda imaš 2 grane rešenja:
X=(pi/2) + 2*k*pi (period T=2*pi)
X=-(pi/2) + 2*k*pi (period T=2*pi)
koje se mogu objediniti u jednu granu X=(pi/2) + k*pi i time se stvara lažnu sliku da je period T=pi.
Ako rešavaš jednačinu:
sin(X) = 0 onda imaš 2 grane rešenja:
X=0 + 2*k*pi (period T=2*pi)
X=pi + 2*k*pi (period T=2*pi)
koje se mogu objediniti u jednu granu X=k*pi i time se stvara lažnu sliku da je period T=pi.
Mislim da su te ovakvi primeri gde je moguće objedinjavanje grana i stvaranje lažne slike da je period T=pi a ne T=2*pi najviše zbunjivali.
Plus činjenica da kad imaš sin(W*X) ili cos(W*X) onda je W*T=2*pi odakle sledi da je period T=(2*pi)/W
Kao u predhodnom Nedeljkovom primeru gde je W=2 pa je 2*T=2*pi odakle sledi da je T=pi.
Nema ni jedne treće situacije, osim objedinjavanja grana rešenja i kad argument nije X već W*X, koja bi mogla kod sin i cos da promeni period da ne bude T=2*pi
[ Nedeljko @ 09.10.2009. 06:51 ] @
Sve je to lepo, samo se ne slažem da je ta slika lažna. Skupo rešenja jednačine 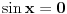 ima period  . Isto važi i za jednačinu  , čiji se skup rešenja može napisati kao 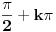 .
Takođe,  je ekvivalentno sa 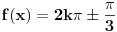 .
Osim toga, česta je greška tretiranje arkus funkcija kao inverza trigornometrijskih funkcija. Trigonometrijske funkcije NISU inverzibilne. Periodična funkcija ne može biti 1-1, pa samim tim ni inverzibilna. Arksu sinus je inverz suženja sinusa na interval 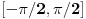 . [ zzzz @ 09.10.2009. 10:22 ] @
Da dodam još i ovo.
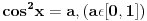
Ovdje funkcija ima period  ,a i rješenja takođe.
Da bi se uvjerili u to najbolje je nacrtati funkciju
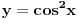 [ Cabo @ 09.10.2009. 19:20 ] @
@zzzz:
Kada pišeš funkcije, kao što su 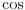 , 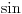 , bilo bi dobro da koristiš naredbe \cos, \sin, itd. Ovako ih 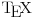 shvata kao proizvode promenljivih  ,  ,  , itd.
Takođe, morao sam da „zabijem nos“ u ekran da bih video da si umesto  ( a\epsilon[0,1]), mislio na 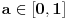 ( a\in[0,1]). :-/
DODATAK:
@Nedeljko: Da, ta zabuna je posledica toga da se funkcije tretiraju kao njihovi izrazi, recimo  u 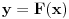 , umesto kao parovi izraza i domena, ovde 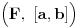 . Funkcije  i 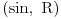 nisu nisu iste.
[Ovu poruku je menjao Cabo dana 09.10.2009. u 21:20 GMT+1][ honijat @ 14.10.2009. 23:59 ] @
@zzzz
Da dodam još i ovo.
cos^2(x)=a,
Ovdje funkcija ima period ,a i rješenja takođe.
Da bi se uvjerili u to najbolje je nacrtati funkciju
y=cos^2(x)
zzzz dali ovo pomaze ?
cos^2(x)
.jpg) [Ovu poruku je menjao honijat dana 15.10.2009. u 01:27 GMT+1]
[Ovu poruku je menjao honijat dana 15.10.2009. u 01:27 GMT+1][ zzzz @ 15.10.2009. 22:43 ] @
Citat: honijat:
zzzz dali ovo pomaze ?
Da.Ovo si lijepo nacrtao.Samo da si dodao horizontalni pravac
y=a i našao presječne tačke sa ovom krivuljom pa sve to zapisao...
.JPG)
[ honijat @ 18.10.2009. 10:43 ] @
Sta odredjuje polozaj prave y=a ?
 [Ovu poruku je menjao honijat dana 19.10.2009. u 00:25 GMT+1]
[Ovu poruku je menjao honijat dana 19.10.2009. u 00:25 GMT+1]
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
| 




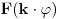
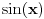

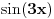
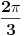
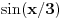
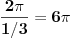
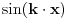
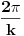

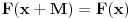
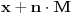
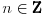
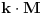
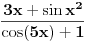
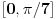
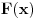
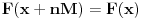
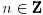
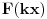
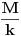
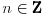
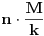
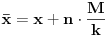
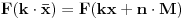
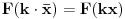
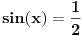
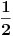
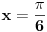
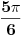
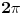
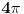
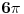
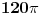
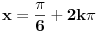
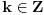
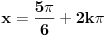

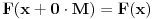
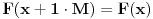
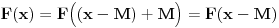
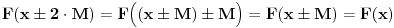
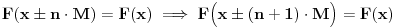
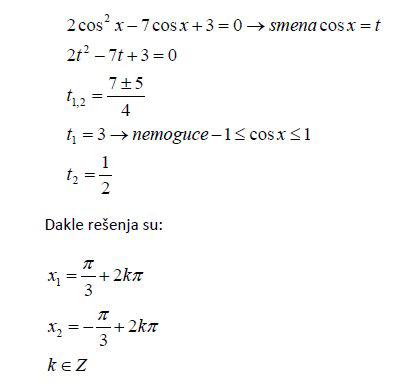


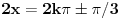


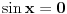

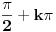

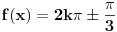
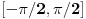
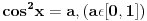
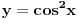
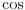
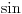
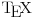




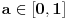
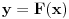
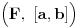

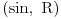
.jpg)
.JPG)
