Ovo nije linearna jednačina. :-S

Uzgred, Matematika daje za realno rešenje , a za kompleksna neka čuda od dve strane.


_{[Ovu poruku je menjao Cabo dana 30.09.2009. u 18:55 GMT+1]}

Jednacine cetvrtog stepena su resive ...

Tačno, ali Matematika ili misli da nisu u , ili nije pojednostavila izraz.

Ostala 4 resenja nisu u R, ali su ipak resiva.
Kad odradimo sve korake za resavanje jed. 4 stepena trebalo bi dobiti nesto poput ovoga: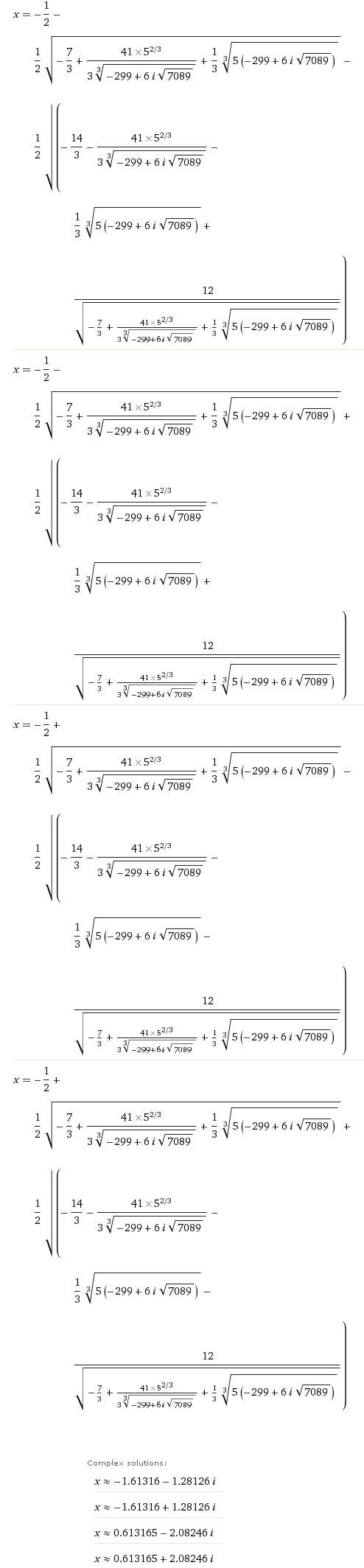

Vidjao sam i lepsa resenja ... ali eto ovde nisu bas podesili

A kako si rastavio x^5+x^3 to me interesuje?

Cabo ti je odgovorio da je preko programa odredio da je jedno resenje 2. Kada znas jedno resenje onda podelis polinom sa x-2 i dobijes polinom cetvrtog stepena.

E sad ako te zanima kako mozes "rucno" da odredis da je jedno resenje 2, jedino sto mi pada na pamet, je preko Hornerove seme.

Ako je dat polinom stepena bar jedan sa celim koeficijentima i slobodnim članom različitim od nule, onda je ma koja (eventualna) racionalna nula tog polinoma količnik celih brojeva od kojih brojilac deli slobodni član polinoma, a imenilac deli vodeći koeficijent polinoma.

Na taj način se dobija konačan skup kandidata za racionalne nule. U ovom slučaju su eventualne racionalne nule polinoma celi brojevi koji dele broj 40. Znači, -40,-20,-10,-8,-5,-4,-2,-1,1,2,4,5,8,10,20,40. Direktnim isprobavanjem se utvrđuje da je 2 koren ovog polinoma.