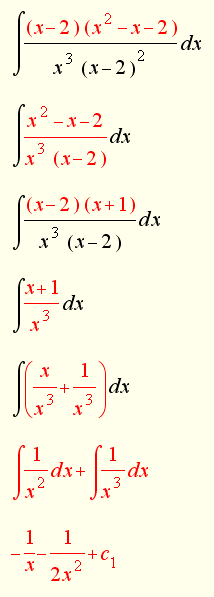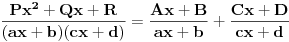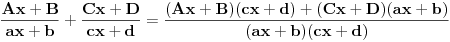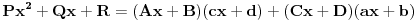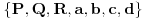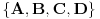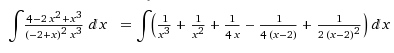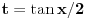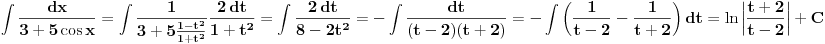[ conver @ 03.10.2009. 12:21 ] @
|
| Pozdrav svima, evo jos jednog integralcica za koji ja ne mogu da se setim kako bese ide rastavljanje na pracijalne razlomke:
∫[(x^3 - 2x^2 + 4) / x^3(x-2)^2 ] dx
dakle ovaj imenilac treba rastaviti [x^3(x-2)^2] jel moze neko da mi pomogne?
ovako to bese:
A/x + B/x^2 + C/x^3 + D/(x-2) + E/(x-2)^2 tako nesto! |
[ igorpet @ 03.10.2009. 14:59 ] @
Mozda je ovako malo lakse i brze, a moze i tako kako si poceo, samo sto ti koeficijenti iznad razlomacke crte nisu svi dobri (gore ide za stepen nize) A/x + (Bx+C)/x^2 + (Dx^2+Ex+F)/x^3 + G/(x-2) + (Hx+I)/(x-2)^2
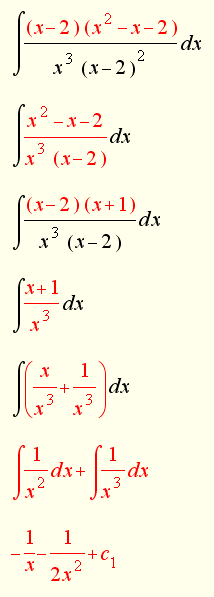
[ Cabo @ 03.10.2009. 17:32 ] @
„Tako nešto“:
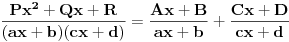
, i sad odrediš

,

,

i

množenjem:
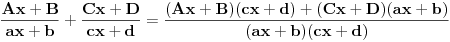
grupisanjem i izjednačavanjem koeficijenata uz stepene

-a u jednakosti
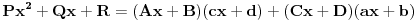
. Poznati su ti
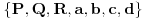
, a trebaju ti
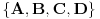
.
[ miki069 @ 05.10.2009. 10:01 ] @
Igore:
X^3 - 2*X^2 +4 nema realnu nulu X=2 i nije jednak onome što si napisao u brojiocu.
Inače conver je rastavio na parcijalne razlomke 100% ispravno.
Priča o B*X+C pije vodu samo ako je ispod puni polinom 2 stepene koji nema realne nule.
Šta će ti (BX)/X^2 to je B/X i to je pokriveno sa A/X
[ igorpet @ 05.10.2009. 11:04 ] @
Citat:
miki069: Igore:
X^3 - 2*X^2 +4 nema realnu nulu X=2 i nije jednak onome što si napisao u brojiocu.
...
Da, u pravu si Miki, ja sam to racunao za x^3-3x^2+4, moja greska, lose prepisao.
X^3 - 2*X^2 +4 ima jednu realnu nulu izmedju -1 i -0.5
Ali nije problem ovo rastaviti na parcijalne razlomke, a i nema autora poruke da nam kaze dokle je stigo ...
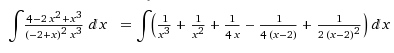
[ Cabo @ 05.10.2009. 11:16 ] @
Ima lepo i vrlo detaljno objašnjeno kod Apsena kako se rade razni tipovi integrala, posebno integrali racionalne funkcije. To je prilično šablonizovano.
[ Nedeljko @ 05.10.2009. 14:00 ] @
Mozda je to uradjeno kod Apsena kako treba, ali je Apsen generalno vrlo losa knjiga, pa ne bi valjalo da se neko navuce na njega zbog obicnog integrala racionalne funkcije, koji je svuda objasnjen kako treba.
[ conver @ 06.10.2009. 10:35 ] @
tu sam momci, tu sam, spremam ispit pa mi je malo guzva....
odradio sam onim algebarskim transformacijama sa slike, lakse mi bilo... no opet me muci jos jedan integral.... do duse nije rastavljanje na parcijlne, ali bih molio za pomoc
∫ dx / 3+5cosx
pokusao sam ono univerzalnom trigonometriJskom smenom tgx/2 = t al ne pije vodu... dakle kako da mrdnem ovo cosx, smeta... smena cosx = t ne moze jer cu ovamo imati izvod kosinusa a to u brojiocu nemam! Hvala!
[ Nedeljko @ 06.10.2009. 10:59 ] @
I sta fali smeni
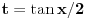
? Naravno da moze preko nje.
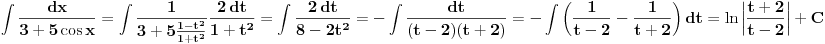
.
[ conver @ 06.10.2009. 16:07 ] @
Ne fali nista, ocigedno, nego sam ja glup... :) hvala Nedeljko!!!
[ Cabo @ 06.10.2009. 18:10 ] @
Citat:
Nedeljko: obicnog integrala racionalne funkcije, koji je svuda objasnjen kako treba.
Da, samo se uz te druge zbirke ljudi javljaju ovde za pomoć. :-/
[ Nedeljko @ 06.10.2009. 20:22 ] @
Pa, za to e treba nikakva zbirka, nego samo udžbenik u kome je dat algoritam, ali eto, ljudi ne umeju da koriste literaturu. Misle da je teorija nešto za davljenje, a ne nešto esencijalnog karaktera, što ima i direktnu upotrebnu vrednost.
Apsenovci ne umeju da urade najelementarnije zadatke, koji zahtevaju samo poznavanje izvoda i tabličnih integrala sa razumevanjem.
@conver
Nisi ti glup, nego si se 3ayebunio. Uz to, fali mi 1/4 ispred poslednjeg rezultata (i sledstveno, algoritma).
[ conver @ 08.10.2009. 12:01 ] @
@igorpet
brojilac nije dobro rastavjen
x^3 - 2x^2 + 4 nije (x-2) * (x^2-x-2)
(x-2) * (x^2-x-2) = x^3-3x^2+4
dakle koeficijenti uz x^2 nisi isti!
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.