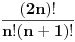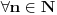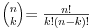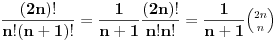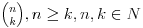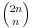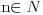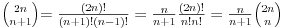[ mathelp @ 07.10.2009. 01:21 ] @
| Naisao sam na zadatak koji sam obavezan za uraditi, a zaista nemam ideju. Ako iko zna, molim vas pomozite! Zadatak glasi ovako: *Dokazite da je (2n)!/(n!(n+1)!) prirodan broj za svako n iz N. Probao sam indukcijom i pretpostavio za n=k, pa sam u trecem koraku za n=k+1 uspio izvuci pretpostavku, ali mi ostaje jos faktora i onda ne znam sta da radim s njima. Unaprijed zahvaljujem! [Ovu poruku je menjao mathelp dana 07.10.2009. u 02:32 GMT+1] |