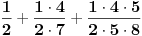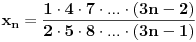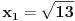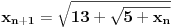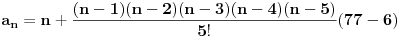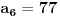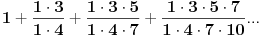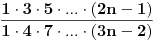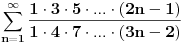[ Kolins Balaban @ 10.10.2009. 16:52 ] @
|
[ Nedeljko @ 10.10.2009. 19:42 ] @
Prvi zadatak nema smisla, jer ima beskonačno mnogo pravila po kojima se dobijaju prva tri člana.
Kod drugog zadatka uoči funkciju 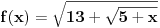 . Očigledno je . Očigledno je 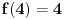 . .Na intervalu 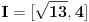 funkcija je rastuća. Odatle se lako dokazuje indukcijom napre da svi članovi niza pripadaju tom intervalu, a onda i da je niz rastući. Stoga on kao rastući i ograničen kora biti konvergentan. Štaviše, limes mora pripadati navedenom intervalu, jer je zatvoren, a svi članovi mu pripadaju. Ali, zbog uslova funkcija je rastuća. Odatle se lako dokazuje indukcijom napre da svi članovi niza pripadaju tom intervalu, a onda i da je niz rastući. Stoga on kao rastući i ograničen kora biti konvergentan. Štaviše, limes mora pripadati navedenom intervalu, jer je zatvoren, a svi članovi mu pripadaju. Ali, zbog uslova 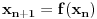 i neprekidnosti funkcije i neprekidnosti funkcije  limes mora zadovoljavati jednačinu limes mora zadovoljavati jednačinu 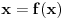 . Na tom intervalu nema drugih rešenja te jednačine, jer bi po Lagranževoj teoremi o srednjoj vrednosti postojala tačka u kojoj je izvod funkcije jednak jedinici, što je u ovom slučaju lako oborivo. . Na tom intervalu nema drugih rešenja te jednačine, jer bi po Lagranževoj teoremi o srednjoj vrednosti postojala tačka u kojoj je izvod funkcije jednak jedinici, što je u ovom slučaju lako oborivo.[ Kolins Balaban @ 11.10.2009. 13:12 ] @
mozes li mi dati neki kontraprimjer za ovaj prvi zadatak. ovaj kolega je na ispitu ponudio isto rjesenje, i prof mu je rekao da nije dobro. sad bih ja da on odnese oba rjesenja, i da kaze da ih ima jos, i da je zadatak nekorektno postavljen....
[ Kolins Balaban @ 12.10.2009. 00:06 ] @
[ lepi.cane @ 12.10.2009. 00:19 ] @
[ Kolins Balaban @ 12.10.2009. 07:36 ] @
u ovoj zbirci se nije trazio dokaz konvergencije, nego samo opsti clan
[ Nedeljko @ 12.10.2009. 07:57 ] @
Izem ti takvu zbirku.
[ Cabo @ 12.10.2009. 10:40 ] @
Citat: Nedeljko: Izem ti takvu zbirku. LOL Takođe, LOL @ Demidovič. Ja sam tu zbirku bukvalno: prelistao, video da ne valja, ostavio da skuplja prašinu. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|