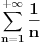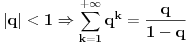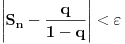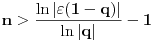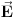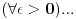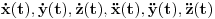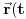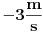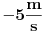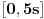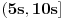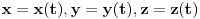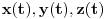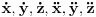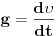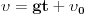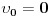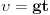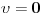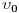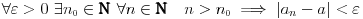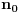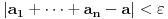|
|
[ TheK @ 11.10.2009. 08:07 ] @
|
| Pozdrav ljudi.
Da li neko može prostim rečima da mi objasni ova dva pojma "konvergira" i "divergira" kod redova?
Imam neke matematičke definicije ali mi nije baš jasno, pa ako neko može malo da pojasni, možda i uz neki primer.
Hvala unapred. |
[ petarm @ 11.10.2009. 09:15 ] @
[ TheK @ 11.10.2009. 09:51 ] @
Ne znam da li sam dobro ukapirao...
Kada neka suma ide ka nekom odredjenom broju, onda se kaže da konvergira, a kada ide ka neodređenom onda divergira?
[ Nedeljko @ 11.10.2009. 10:25 ] @
Divergira ako ne konvergira. A šta ti znači "ide ka nekom broju"?
Ljudi, shvatite, kada bi neko našao jednostavniju definiciju konvergencije brojnih redova od postojeće, matematičari bi je prvi koristili. Uvek se teži pojednostavljivanju, ako je moguće. O ovome su matematičari razmišljali preko 100 godina (standardno zasnivanje analize je završeno radovima Kantora i Dedekinda, koji se odnose na zasnivanje realnih brojeva, još 1872/73 godine). Da je neko našao prostiju definiciju, ona bi bila u upotrebi.ž To je akao kada bi otišli u prodavnicu automobila i pitali imaju li nešto za 50 evra za studente i penzionere - nema.
[ TheK @ 11.10.2009. 10:45 ] @
Citat: Nedeljko: Divergira ako ne konvergira. A šta ti znači "ide ka nekom broju"?
Pa npr. iz ovog primera:

Ja samo pitam da mi neko objasni onako kako je on razumeo, a bez matematičih definicija, znači svojim rečima.
Lako ću ja to kasnije dopuniti... [ anon142305 @ 11.10.2009. 11:05 ] @
A da li bi moglo da bude ovako, laicki gledano?
Konvergira: kako "ide" red, svaki sledeci clan je sve blizi i blizi prethodnom, odnosno red postaje sve vise zgusnut.
Divergira bi bio ako postaje sve "redji i redji".
[ Mikky @ 11.10.2009. 11:51 ] @
Citat: TheK: Ne znam da li sam dobro ukapirao...
Kada neka suma ide ka nekom odredjenom broju, onda se kaže da konvergira, a kada ide ka neodređenom onda divergira?
Za "opusteniju" verziju definicije mozes da koristis to sto si rekao. Za striktno matematicku koju ces reci profesoru moras ipak da koristis onu iz udzbenika. [ igorpet @ 11.10.2009. 13:50 ] @
Citat: TheK: Pozdrav ljudi.
Da li neko može prostim rečima da mi objasni ova dva pojma "konvergira" i "divergira" kod redova?
...
Pa evo i ja da pripomognem jednim prostim primerom:
-----------------------------------------
zašto niz plavuša konvergira?
jer je ograničen i monoton
-----------------------------------------
  [ Nedeljko @ 11.10.2009. 14:47 ] @
Citat: IUOP_1: A da li bi moglo da bude ovako, laicki gledano?
Konvergira: kako "ide" red, svaki sledeci clan je sve blizi i blizi prethodnom, odnosno red postaje sve vise zgusnut.
Divergira bi bio ako postaje sve "redji i redji". 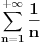 je divergentan red. Rekoh, ako i može prostije, to niko nije uspeo da pronađe. U protivnom bio objavio rad, barem metodološki, ako ne naučni i radilo bi se tako. Kada bi se znalo prostije, tako bi se i radilo. [ anon142305 @ 11.10.2009. 15:13 ] @
@ Nedeljko
Covek je pitao kako je ko razumeo te pojmove, a nije trazio najprostiju matematicku definiciju!
[ TheK @ 11.10.2009. 16:50 ] @
Ok, evo konkretan primer, pa bih zamolio ako neko moze da pokaze kako se radi:
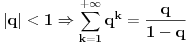 [ Nedeljko @ 11.10.2009. 17:31 ] @
Citat: IUOP_1: @ Nedeljko
Covek je pitao kako je ko razumeo te pojmove, a nije trazio najprostiju matematicku definiciju!
Pitao je da mu se prostim rečima kaže šta znače ti pojmovi. Matematičari su to uprostili koliko su umeli. Svako dalje uprošćavanje bilo bi značajan pomak napred.
Dakle, ovako, delimična suma tog reda je  , što se dokazuje indukcijom. Stoga je  . Neka je dato  . Nas zanima kada je 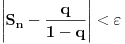 . Ta nejednačina je ekvivalentna sa 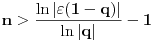 , pa ako izaberemo bilo koje  , važiće 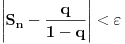 za svako  . Drugim rečima, nejednakost 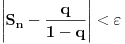 važi pošev odnekle, pa nadalje. To je zato što je ekvivalentna nejednakosti 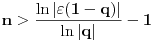 , koja očigledno važi počev odnekle, pa nadalje. [ TheK @ 11.10.2009. 17:47 ] @
Stvarno hvala puno na pomoći!
[ Cabo @ 11.10.2009. 18:29 ] @
Kada su pitali jednog poznatog matematičara (kao za inat ne mogu trenutno da se setim koga tačno; Gausa? Njutna? Nije bitno.) kako je došao do svojih otkrića, odgovorio je:
„Neprestano sam mislio o tome.“
Tako je i kod shvatanja osnovnih matematičkih pojmova. Osnovna stvar kod Analize je shvatiti odnos beskonačnih i konačnih veličina. Sve se vrti oko toga: tačke nagomilavanja, konvergencija, diferencijabilnost, redovi, razvoji...
[ petarm @ 17.10.2009. 10:52 ] @
Sve su to bili fizičari!
[ Nedeljko @ 17.10.2009. 11:01 ] @
Ma, daj molim te.
Neki ljudi su se aktivno bavili matematikom, fizikom i astronomijom, kao na primer Gaus u Njutn, s tim što ej Gaus bio na prvom mestu matematičar, a Njutn na prvom mestu fizičar. Lajbnic se aktivno bavio matematikom i filozofijom. Za Gausa i Njutna se ne može reći da su bili fizičari koji su dali doprinos matematici, kao što se za Lajbnica ne može reći da je bio filozof koji je dao doprinos matematici.
Druga je stvar Furije, koji se nije bavio matematikom kao takvom, već fizikom, a unapredio je matematiku. On jeste bio fizičar koji je unapredio matematiku, ali tvrditi tako nešto za Gausa i njutna nije osnovano.
[ petarm @ 17.10.2009. 11:26 ] @
Njutn je došao do integrala jer mu je bilo potrebno da izračuna gravitaciono privlačenje 2 kugle. I Lajbnic i on su se bavili primenom diferencijalnog i integralnog računa u mehanici kao i kasnije Ojler, Hamilton i Lagranž. Sofija Kovalevska se isto tako bavila primenom u mehanici. Isto tako
 - Gausov zakon
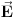 - vektor električnog polja
Ne kažem svi oni su se bavili i matematikom. Ali su je primenjivali na konkretne probleme iz prirode, koju su pokušavali da objasne. I to ih čini fizičarima fizis=priroda.
Ima naravno i jako puno čistih matematičara u istoriji koji su dali ogroman doprinos kao npr. Evaris Galoa, Karl Vajerštras, David Hilbert... Ali diferencijalni i integralni račun su definitivno tvorevina fizičara.
Matematičari rade jedan sjajan posao, ja ne kažem to. Dovode mnogo stvari na svoje mesto, uopštavaju ih... dolaze do novih stvari...
Recimo način zapisivanja koji je mislim potekao od Vajerštrasa
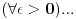
i sve dalje urađeno u ovakvom zasnivanju matematičke teorije pripada naravno matematičarima, ali to što je Cabo naveo u prethodnoj poruci je definitivno delo fizičara.
[ Nedeljko @ 17.10.2009. 11:54 ] @
Jesu li Njutnu trebali binomna formula i metod tangente za mehaniku? Ma, daj molim te, Njutn jeste bio na prvom mestu fizičar, ali se bavio i matematikom nezavisno od fizike, a ne samo za potrebe fizike. Što se diferencijalnog računa tiče, dok se Lajbnic bavio primenama, Njutn se bavio teološkim tumačenjima istog. Beskonačnost, pa Bog, pa sve na "B". Nađi mi u Njutnovoj mehanici (ona čuvena "Principia") izvod! Tamo je izveo zakon gravitacije iz Keplerovih zakona, bez diferencijalnog i integralnog računa.
A što se Gausa tiče, koji je na prvom mestu bio matematičar, ovo je tek smešno. Kakve veze ima konstruktibilnost pravilnih poligona lenjirom i šestarom sa mehanikom? Kakve veze ima teorija brojeva sa mehanikom?
Podvlačim, Gaus i Njutn su se bavili matematikom i nezavisno od fizike, za razliku od Furijea i Ajnštajna.
[ petarm @ 17.10.2009. 12:10 ] @
Citat: Nedeljko: Jesu li Njutnu trebali binomna formula i metod tangente za mehaniku? Ma, daj molim te, Njutn jeste bio na prvom mestu fizičar, ali se bavio i matematikom nezavisno od fizike, a ne samo za potrebe fizike.
Odgovor je jesu!
Citat: Nedeljko: Tamo je izveo zakon gravitacije iz Keplerovih zakona, bez diferencijalnog i integralnog računa.
Ne nalazi se sve u Njutnovom delu "Principia Mathematica Philosophia Naturalis". On je ovo delo napisao 1687., a umro je 1727.
Most modern historians believe that Newton and Leibniz developed infinitesimal calculus independently, using their own unique notations. According to Newton's inner circle, Newton had worked out his method years before Leibniz, yet (according to one view) he published almost nothing about it until 1693, and did not give a full account until 1704.
Integral mu je trebao za tretiranje gravitacionog privlačenja kugli. Za gravitaciono privlačenje 2 tačkaste mase mu nije trebao integral.
Citat: Nedeljko:
A što se Gausa tiče, koji je na prvom mestu bio matematičar, ovo je tek smešno. Kakve veze ima konstruktibilnost pravilnih poligona lenjirom i šestarom sa mehanikom? Kakve veze ima teorija brojeva sa mehanikom?
Podvlačim, Gaus i Njutn su se bavili matematikom i nezavisno od fizike, za razliku od Furijea i Ajnštajna.
Slažem se za Gausa. Prihvatam. Ali on svakako nije ni rekao ono što je napisao Cabo. [ Nedeljko @ 17.10.2009. 12:56 ] @
Njutnov metod tangente nema nikakve veze sa fizikom. To je kao kada bi rekao da su algoritmi za sabiranje, oduzmanje i množenje fizički orjentisani zato što ih fizičari koriste prilikom računanja. To su opšte matematičke stvari.
Kada se kaže da je neki matematički doprinos delo fizičara, podrazumeva se da taj fizičar nije bio matematičar, što se za Njutna, a pogotovu Lajbnica, ne može reći. Zaboravio si na Lajbnicov metod određivanja lokalnih ekstremuma preko izvoda. Takođe, površine i zapremine su čisto matematički pojmovi, bez obzira što ih još poneko koristi.
[ petarm @ 17.10.2009. 13:26 ] @
Ali mu je trebao da reši numerički neku jednačinu koja je nastala iz fizičkog problema. (To je kao kada bi rekao da je Dirak matematičar zbog  funkcije.) Inače ne bi ni došao do toga. Stvari su danas mnogo lakše jer je već jako puno stvari u matematici urađeno. Veliki broj fizičara koji su živeli u 20. veku bili bi nazvani matematičarima da su živeli u 18.,19. npr. Njutn je bio fizičar koji je veoma doprineo razvoju matematike.
Citat: Nedeljko:
Zaboravio si na Lajbnicov metod određivanja lokalnih ekstremuma preko izvoda. Takođe, površine i zapremine su čisto matematički pojmovi, bez obzira što ih još poneko koristi.
Mene zanima da li znaš kako je on došao do toga. Jel je seo jedan dan u park i rekao baš mi je dosadno, ajd da smislim neki metod određivanja lokalnih ekstrema uz pomoć izvoda koji će biti nazvan po meni.
Ti imas tehniku računanja integrala pomoću Fajnmanovih dijagrama. Jel je Fajnman sad i matematičar ili nije?
Braun je otkrio posmatranjem neki zrna polena (negde kažu sporangija paprati) haotično kretanje koje je nazvano Braunovo kretanje. U svakoj knjizi iz fizike u kojoj je ovo obređeno videćes da piše da je Braun botaničar.
http://www.aip.org/history/einstein/essay-brownian.htm
[ Nedeljko @ 17.10.2009. 13:57 ] @
Ričard Fejman je čist fizičar i veliko ime. Šta god da je smislio, svaka mu čast, ali nije matematičar. Prihvatam da je dao doprinos matematici kao čist fizičar.
No, Njutnov metod tangente je numerički metod, a to je opšta stvar. Mogu ga koristiti i ekonomisti i inženjer, kome god zatreba. Nije vezana za fiziku. Ja ne osporavam da su ljudi dali doprinose van oblasti kojima su se bavili, ali tvrdim da su Njutn i Lajbnic bili matematičari, a ne nematematičari, tj. da su se bavili matematikom i nezavisno od fizike.
[ petarm @ 17.10.2009. 15:00 ] @
Prihvatam ovo što kažeš. Da je Njutn bio i fizičar i matematičar. Ušao je i u jedne i u druge knjige. Naravno na prvom mestu je fizičar. Ipak
Citat: Cabo: Kada su pitali jednog poznatog matematičara (kao za inat ne mogu trenutno da se setim koga tačno; Gausa? Njutna? Nije bitno.) kako je došao do svojih otkrića, odgovorio je:
„Neprestano sam mislio o tome.“
Tako je i kod shvatanja osnovnih matematičkih pojmova. Osnovna stvar kod Analize je shvatiti odnos beskonačnih i konačnih veličina. Sve se vrti oko toga: tačke nagomilavanja, konvergencija, diferencijabilnost, redovi, razvoji...
o ovim stvarima on je razmišljao sa aspekta fizičara. I mislim da je to jako dobro. I da tako te pojmove treba i uvoditi.

I razmišljao je o tome na ovaj način. Šta je trenutna brzina?
[ Nedeljko @ 17.10.2009. 15:28 ] @
Da li je brzina fizički ili matematički pojam? Za mene fizika počinje sa dinamikom. Kinematika je u suštini deo geometrije. Tek sa silama, impuslima, pritiscima itd. počinje fizika.
[ Nemanjich @ 17.10.2009. 15:49 ] @
Pa Nedeljko, geometrija ne poznaje pojam vremena. Moze se uvesti neki parametar koji ce mozda nekako imati ulogu vremena, ali nece biti to. U mom udzbeniku za fiziku 1, za kinematiku se kaze da je geometrija sa vremenom, gde je vreme fizicki pojam.
Sa druge strane fizika ne moze nigde(skoro) da mrdne bez geometrije, mada ovo nije tema za to.
Pozdrav!
[ petarm @ 17.10.2009. 15:54 ] @
Već u kinematici ti uvodiš određene aproksimacije. Materijalna tačka nije matematička tačka. Kada su dimenzije tela zanemarljive u odnosu na dimenzije oblasti u kojoj se ono kreće mi ga možemo smatrati materijalnom tačkom. A ta materijalna tačka ima neka fizička svojstva kao npr. masu. Ako to ne važi ti nemaš tu aproksimaciju. Isto tako imaš i kinematiku krutog tela koje je jedna idealizacija nedeformabilnog tela. Kinematika je deo mehanike koji istina proučava promenu položaja tela, ali u vremenu tako da tu nema govora o matematici. Na većini tehničkih fakulteta se recimo prvo rade Statika, Kinematika pa Dinamika. Gde na Statici već uvodiš pojam sile, ravnoteže, momenta sile...
[ petarm @ 17.10.2009. 16:02 ] @
Nedeljko razmišlja na sledeći način. Ali ja ću vreme posmatrati kao nezavisnu promenljivu. Suština je da ja vreme mogu da merim štopericom i da fizički interpretiram šta mi to znači trenutna brzina. I da razumem gornji limes!
[ petarm @ 17.10.2009. 16:14 ] @
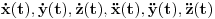 ne moraju biti neprekidne fje vremena. Npr. kad se čestica odbije od neke površi komponenta brzine normalna na površ trpi skok. Ili posmatraj kretanje autobusa pri kočenju! Ovo mi diktira fizika! Ja čitajući fizički tekst krećem da rešavam zadatak. Npr. metak ispaljen u drvo debljine 1m ne izleti iz istog. Ja pišem neke jednačine za ovo, ali njih mi diktira priroda. [ Nedeljko @ 17.10.2009. 18:17 ] @
Citat: Nemanjich: Pa Nedeljko, geometrija ne poznaje pojam vremena.
Ja sam učio pojam brzine iz predmeta "diferencijalna geometrija". Dakle, glatka kriva je glatko preslikavanje r nekog intervala iz R u R n, a ako pritom izvod nije jednak nuli ni u jednoj tački, onda se za tu krivu kaže da je regularna. Izvod r'(t) je vektor brzine krive r u tački t, a njegov intenzitet je brzina krive u tački t.
Dakle, nigde nema ni materijalne tačke, ni vremena, ni štoperice.
Citat: petarm: Npr. kad se čestica odbije od neke površi komponenta brzine normalna na površ trpi skok.
Jesi li siguran da u fizici brzina zaista može da trpi skok? Ja bih pre rekao da je to eventualno svojstveno ubrzanju, ali, ti si svakako kompetentniji. No, to nema veze sa ovim. [ Nedeljko @ 17.10.2009. 18:49 ] @
Nego, da se ne bismo više preucavali, ovde je očigledno sporan pojam matematike. Kako je vi shvatate?
[ Nemanjich @ 17.10.2009. 19:20 ] @
Tesko pitanje Nedeljko, tesko da se da normalan odgovor. Al' 'ajde:
Matematiku shvatam kao nesto najapstraktnije, u cemu i lezi njena lepota po meni. Nesto sto generalizuje intuitivne ideje (najcesce "prirodne"), i dolazi do neverovatnih zakljucaka, npr visedimenzionalna geometrija(Za koju je cini mi se Kant dao dokaz da ne moze postojati vise od tri dimenzije.toliko o njemu.). Iskreno za sada, krivo mi je sto nemam neko vece znanje nje same, posto bih jako voleo da ovladam analitickim pristupom neeuklidskim geometrijama, koje su po meni nesto jako fino.
Ove je neki nekakav odgovor, dobar ne verujem, al' je ipak odgovor.
[ Cabo @ 17.10.2009. 19:21 ] @
Proverio sam, u pitanju je Njutn! 
Inače, citat sam video u Merkleovoj zbirci iz Analize.  DODATAK:
DODATAK:
@Nemanjich:
Zavisi šta se smatra dimenzijom. [ petarm @ 17.10.2009. 19:28 ] @
Citat: Nedeljko:
Nego, da se ne bismo više preucavali, ovde je očigledno sporan pojam matematike. Kako je vi shvatate?
Otvori novu temu!
Citat: Nedeljko: Jesi li siguran da u fizici brzina zaista može da trpi skok? Ja bih pre rekao da je to eventualno svojstveno ubrzanju, ali, ti si svakako kompetentniji. No, to nema veze sa ovim.
Zašto ne bi mogla da trpi skok. Voziš automobil i naglo zakočiš. Hoćeš da kažeš da brzina ne trpi skok? To je druga stvar što u mnogim knjigama se na pošetku kaže neka su 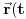 i  neprekidne i diferencijabilne funkcije... Pa se onda dalje raspisuje teorija. Jer nam je naravno u tom slučaju život lep! Tako je to u mnogim mehanikama pisanim i za fizičare i za inženjere. [ Nemanjich @ 17.10.2009. 19:47 ] @
@Cabo
Prostorne, nama tri poznate....
[ Nedeljko @ 17.10.2009. 21:36 ] @
Citat: petarm: Zašto ne bi mogla da trpi skok. Voziš automobil i naglo zakočiš. Hoćeš da kažeš da brzina ne trpi skok?
Pa, nisam primetio da automobil može da stane u mestu. Brzina se postepeno smanjuje tokom nekog vremena do nule. To svakako nije primer skokovite promene brzine. Kada se loptica odbije od zida, svakako ni ona ni zid nisu apsolutno kruti. Opet se brzina menja postepeno. [ Nedeljko @ 17.10.2009. 21:43 ] @
Dobro, ne moramo da otvaramo novu temu o matematici, ali to što je neko crpeo inspiraciju odnekle ne znači da to nije razmišljanje matematičara. Ako ćemo mak na konac, geometrija je crpela inspiraciju iz poljoprivrede, astronomija iz astrologije itd. Dokle bismo tako stigli?
[ petarm @ 17.10.2009. 22:29 ] @
Citat: Nedeljko: Brzina se postepeno smanjuje tokom nekog vremena do nule. To svakako nije primer skokovite promene brzine. Kada se loptica odbije od zida, svakako ni ona ni zid nisu apsolutno kruti. Opet se brzina menja postepeno. Citat: petarm: Npr. kad se čestica odbije od neke površi komponenta brzine normalna na površ trpi skok.
Promeniće se od  na npr. 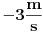 . Čestica će krenuti da se kreće u suprotnom smeru.
A pri naglom kočenju brzina neće u trenutku pasti na nulu, ali će pretrpeti skok.
[Ovu poruku je menjao petarm dana 18.10.2009. u 00:01 GMT+1][ Nedeljko @ 17.10.2009. 23:15 ] @
Citat: petarm: Promeniće se od  na npr. 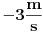 . Čestica će krenuti da se kreće u suprotnom smeru.
Taj deo sa komponentom normalnom na površ si mogao da preskočiš, jer ako je komponenta paralelna sa površi ista, a komponenta normalna na površ se skokovito promeni, onda će se i ukupan intenzitet brzine naglo promeniti.
Nego, daj ti meni konkretan slučaj toga. Od čega je ta površ? Zar nije i ona sačinjena od čestica? Kakav je sudar dveju čestica? Da li se išta zna na datu temu, ili se sudar dva neutrona aproksimira kao skokovita promena brzine? [ Nedeljko @ 17.10.2009. 23:23 ] @
Citat: petarm: A pri naglom kočenju brzina neće u trenutku pasti na nulu, ali će pretrpeti skok.
Ovaj deo mi tek nije jasan, ali ni najmanje. [ petarm @ 17.10.2009. 23:47 ] @
Citat: Nedeljko: Taj deo sa komponentom normalnom na površ si mogao da preskočiš, jer ako je komponenta paralelna sa površi ista, a komponenta normalna na površ se skokovito promeni, onda će se i ukupan intenzitet brzine naglo promeniti.
Nego, daj ti meni konkretan slučaj toga. Od čega je ta površ? Zar nije i ona sačinjena od čestica? Kakav je sudar dveju čestica? Da li se išta zna na datu temu, ili se sudar dva neutrona aproksimira kao skokovita promena brzine?
OK! Neka je sudar elastičan između čestice i zida. Neka čestica udari u zid brzinom  . Njena brzina nakon odbijanja će biti 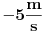 . Neka se npr. u intervalu vremena 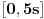 telo kreće brzinom  , a od 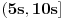 sa 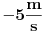 . Nacrtaj grafik  . Je li ovo prekidna funkcija?
Sudar dva neutrona ne možeš razmatrati u okviru klasične fizike. Sudare u fizici tretiraš preko zakona održanja impulsa. I ako je sudar elastičan koristiš i zakon održanja energije. Pa kažeš impuls pre sudara jednak je impulsu posle sudara...
[Ovu poruku je menjao petarm dana 18.10.2009. u 02:19 GMT+1][ Nedeljko @ 17.10.2009. 23:53 ] @
Ma, jeste to prekidna funkcija, ali ja mislim da se taj slučaj nikada ne dešava u prirodi.
Recimo, loptica stiže do zida, onda se loptica i zid deformišu, loptica smanjuje postepeno brzinu, dolazi do vraćanja prvobitnog oblika zida i loptice, loptica menja smer i postepeno dobija brzinu. Dakle, sve postepeno.
[ petarm @ 20.10.2009. 11:05 ] @
Evo da citiram Bozidara Milica udzbenik Njutnova mehanika.
9 str.
''U Njutnovoj mehanici se principijelno iskljucuje mogucnost takvih kretanja u toku kojih bi cestica mogla da dospe iz jedne tacke prostora u drugu, a da pritom ne prodje kroz sve tacke duz neke linije koja te tacke spaja. Dakle, iskljucuju se kretanja u toku kojih bi cestica ''preskocila'' sa jednog mesta na drugo. Istaknimo da iz toga ne sledi da funkcije
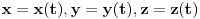
moraju biti i diferencijabilne. Kuglica koja udara u zid i odbija se je primer za ovo. ''
10 str.
''Za razliku od funkcija 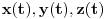 komponente brzine i ubrzanja, tj. funkcije 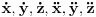 ne moraju biti neprekidne funkcije vremena. Na primer, kada se cestica odbija od neke povrsine, komponenta njene brzine normalna na povrsinu trpi u momentu udara konacan skok, dok odgovarajuca komponenta ubrzanja trpi beskonacan skok''. [ Nedeljko @ 20.10.2009. 14:33 ] @
Ma, to su Njutnove aproksimacije, ali u prirodi nije tako.
[ petarm @ 20.10.2009. 16:50 ] @
Cela fizika jeste neka aproksimacija prirode. U kinematiku su ugradjene linearne diferencijalne jednacine. Sto znaci ako znas polozaj cestice u jednom trenutku znaces ga i u svakom sledecem. Na neki nacin postajes prorok! Kada razmatras slobodan pad
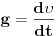
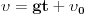
Kod slobodnog pada 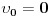 pa je
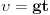
Kad lopta npr. udari o pod ja cu zaustaviti stopericu i na osnovu gornje formule reci lopta je udarila o zemlju tom i tom brzinom. Naravno usled ovog udara u prirodi ta lopta nece stici do iste visine pri odskoku. Ono sto sigurno znam da maksimalna visina odgovara polozaju 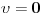 , pa cu odatle lako izracunati 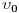 pri kretanju navise. I ovo ce vrlo lepo opisivati prirodu u nekoj vakuumskoj prostoriji. Cak i u vazduhu ako posmatramo kuglice male zapremine. Fizika nije egzaktna nauka u smislu da kaze ovo je tacna vrednost toga i toga vec u smislu ovo je izmereno s tom i tom greskom... Ako se tvoja teorija poklapa sa eksperimentom onda je ona dobra i samim tim da dobro opisuje prirodu.
Klasicna mehanika je zapravo jedan domen fizike. Mi sada pricamo o kinematici. Tu ne pricamo o tome sta je uzrok tome sto se desilo. Ako hoces da ovaj sudar razmatramo na mikro- nivou onda to nije klasicna vec kvantna fizika - drugi domen u kojoj recimo trajektorija cestica nema smisla... Danas se ovom vrstom mehanike bave masinci. Oni prave sve te silne skalamerije i veruj mi da je vec pokazano da je ova mehanika o kojoj ti i ja pricamo dobra teorija.
[ Nedeljko @ 20.10.2009. 17:09 ] @
Sve je to meni jasno. Sve je to OK i to sam znao od ranije.
Međutim, danas postoje opštije fizičke teorije višeg stepena tačnosti od klasične mehanike. Mene zanima trenutno preovlađujuće mišljenje među naučnicima kakvo je kretanje u prirodi zaista - može li se brzina skokovito menjati. Ako nisam dovoljno precizan, onda kako stoje stvari sa tim u najopštijim teorijama koje to opisuju. Možemo mi zanemariti u nekom zadatku elastičnost loptice i zida, ali šta naučnici misle o onome što se zaista dešava u prirodi?
[ petarm @ 20.10.2009. 18:40 ] @
Uzmi trajektoriju kuglice koja udara o zid. Na mesto udara kuglice trajektorija ima dve tangente, pri kosom padanju kuglice.
[ Nedeljko @ 20.10.2009. 20:56 ] @
Celo vreme imam utisak da ne razumeš šta te pitam.
Govoriš li o realnoj kuglici i realnom zidu u prirodi, koji imaju elastičnost, ili o idealizovanom slučaju na papiru apsolutno krutog zida i apsolutno krute kuglice?
OK, od kog materijala su kuglica i zid? Od čega god da je kuglica, ona ima stišljivost i elastičnost. Taj idealan slučaj o kome govoriš postoji smo na papiru. U prirodi ne.
[ honijat @ 21.10.2009. 00:08 ] @
Ljudi pa vi ste na temi Konvergira, divergira i covek vas je samo zamolio za jednostavno objasnjenje tih termina a vi se sjatili da mu na brzaka date neke formule i objasnjenje da su to matematicari vec do kraja pojednostavili.A on da je razumeo te formule ne bi vas ni pitao.
Mogli ste coveku bar malo da se ozbiljnije upustite u objasnjenje sta KONVEGGENCIJA (priblizavanje ) a sta DIVERGENCIJA (udaljavanje) u matematici znaci.
Ne bi zeleo da se naljutite ali ovo o cemu vi sada raspravljate je u stvari prepirka ko je pametniji,a ja sam vec jednom rekao da vi zbog dobrog poznavanja materije niste u stanju da stvar saopstite tako da to razume onaj ko pita a pita uvek onaj ko nezna.
[Ovu poruku je menjao honijat dana 21.10.2009. u 01:21 GMT+1]
[ Fitopatolog @ 21.10.2009. 09:01 ] @
Citat: honijat: Ljudi pa vi ste na temi Konvergira, divergira
Pa eto, to je primer za DIVERGIRA (od teme...) [ Cabo @ 21.10.2009. 09:46 ] @
Citat: honijat: Ljudi pa vi ste na temi Konvergira, divergira i covek vas je samo zamolio za jednostavno objasnjenje tih termina a vi se sjatili da mu na brzaka date neke formule
Matematika se izražava formulama. Šta su formule? Način da se komplikovaniji tekstualni izraz kraće zapiše.
Niz konvergira: 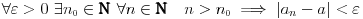
Rečima: niz konvergira ako se za svaku pozitivnu veličinu  može naći prirodni broj 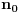 , takav da je udaljenost svih članova niza  od neke realne vrednosti  , za sve prirodne brojeve  veće od njega, manja od  .
Ne može „lakše“. Nije ovo osnovna školica, već fakultetsko gradivo. Nauka, bre! [ Nedeljko @ 21.10.2009. 10:19 ] @
@honijat
Šta ako ne može lakše? Šta misliš, kad bi postojao lakši način, da ne bi on bio u upotrebi umesto ovog?
[ honijat @ 21.10.2009. 21:31 ] @
Vi ste potpuno upravu kada tvrdite da su formule naj jednostavniji zapis svakok matematickog problema ali se do formula doslo prvo razgovorom u timu ili razmisljanjem sam sa sobom a i razmisljanje je vid razgovora sa samim sobom .Nemoj pomisliti da ja pokusavam da ovde drzim predavanje nego samo pokusavam da kazem da mnogi vole o temi koju ne razumeju da popricaju sa ljudima u koje imaju poverenje, a mi ovde imamo prilicno opravdano poverenje u vas jer smo dobili dosta pomoci od vas naravno to i ocekujemo kada posetimo forum matematike a nadam se da i vama cini zadovoljstvo da to svoje znanje nekome delite.Niko ne mora da odgovara ukoliko mu to nekad nije po volji ali mislim da nije fer coveku koji trazi pomoc oko Konvegira,divergira dati odgovor ako ne konvergira onda divergira i covek se pri tom jos i lepo zahvalio a siguran sam da zna isto onoliko koliko je znao i pre odgovora .
[ Cabo @ 21.10.2009. 22:12 ] @
Citat: honijat: Vi ste potpuno upravu
Ma, ceo government...  (Nisam mogao da odolim.)
Citat: honijat: covek se pri tom jos i lepo zahvalio a siguran sam da zna isto onoliko koliko je znao i pre odgovora .
Ne može prostije. Sve je svedeno na najprostije činioce i dalje ne ide. Didaktički, još samo mogu da se daju primeri, a njih ima obilje u udžbenicima Analize. Ako neko i pored toga ne razume, šta tu mi možemo. Niko nije primoran da se bavi matematikom, što ne znači da nije izuzetno talentovan u nekoj drugoj disciplini. [ Nedeljko @ 22.10.2009. 00:17 ] @
Da, red divergira ako ne konvergira. To je definicija divergencije.
Definicija konvergencije ka broju  je da za ma koje realno  postoji prirodan broj 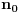 takav da za ma koje  važi 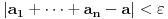 .
Mi ne znamo prostije od toga. Ako ti znaš, izvoli. Mislim da ćeš ući u udžbenike matematike. [ Cabo @ 22.10.2009. 19:05 ] @
Definicija divergencije niza je negacija definicije konvergencije niza:
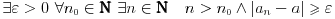 [ petarm @ 23.10.2009. 23:14 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|