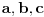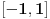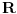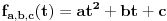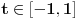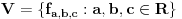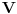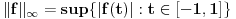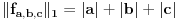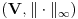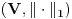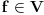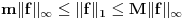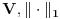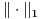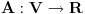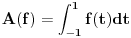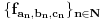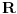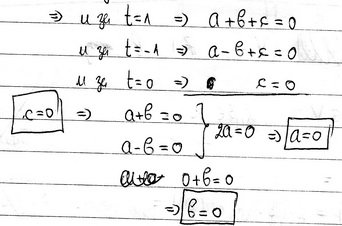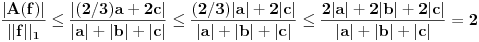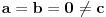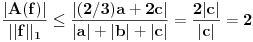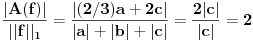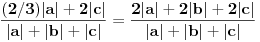[ lepi.cane @ 11.10.2009. 21:08 ] @
|
[ Nedeljko @ 11.10.2009. 22:13 ] @
Prvi način:
Ako niz 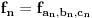 konvergira, onda konvergira i niz konvergira, onda konvergira i niz 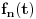 za bilo koje za bilo koje 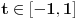 Posmatraj tri vrednosti za Posmatraj tri vrednosti za  , recimo 0,1,-1. Interpolacionom formulom se , recimo 0,1,-1. Interpolacionom formulom se 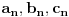 izražavaju preko izražavaju preko 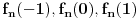 . Recimo, . Recimo, 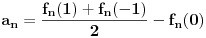 , , 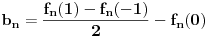 , , 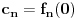 . .Drugi način: Vidi teoriju. Svake dve norme na konačnodimenzionom prostoru su ekvivalentne i svaki konačnodimenzioni normirani prostor je Banahov. [ lepi.cane @ 11.10.2009. 22:43 ] @
Imao sam ideju sa t=-1, t=0 i t=1, ali nije mi palo na pamet ono sa izražavanjem
 , , 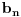 i i 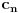 preko preko 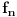 . Hvala u svakom slučaju. Znam za tu teoremu, ali tek stavka pod f) pokazuje da je V konačno dimenzioni prostor, tako da je pod c) ne mogu koristiti. . Hvala u svakom slučaju. Znam za tu teoremu, ali tek stavka pod f) pokazuje da je V konačno dimenzioni prostor, tako da je pod c) ne mogu koristiti. Kao što se vidi ovo mi je dalo samo konvergenciju 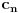 , ali za ostale nije uspelo ni u kojoj kombinaciji. , ali za ostale nije uspelo ni u kojoj kombinaciji.[ Nedeljko @ 11.10.2009. 22:56 ] @
a+b+c=f(1)
a-b+c=f(-1) c=f(0) Dakle, sistem linearnih jednačina. [ lepi.cane @ 11.10.2009. 22:56 ] @
[ Nedeljko @ 11.10.2009. 23:07 ] @
Kurtališi se te gospode, molim te!
[ lepi.cane @ 11.10.2009. 23:11 ] @
Mogao sam i sa "hvala ti Neđo, brate" ali nekako mi je draže ono što sam prvi put napisao, sem toga već dva puta dobijam ogromnu pomoć od Vas, pa je red da se, ako ništa drugo, bar lepo i kulturno zahvalim.
[ Nedeljko @ 11.10.2009. 23:12 ] @
Citat: lepi.cane: Sličnu ideju sam koristio pri dokazu da je 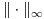 norma kod aksiome N1 norma kod aksiome N1Ma, jok, to ti nije bilo potrebno. Dovoljno je znati da je 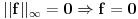 , jer , jer  nije skup trojki nije skup trojki 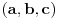 , već skup funkcija! , već skup funkcija!No, može i tako, ali si onda nepotrebno zakomplikovo rešenje. Tako bi se radilo da ti je na taj način zadata norma u skupu trojki realnih brojeva 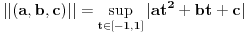 . .[ Nedeljko @ 11.10.2009. 23:13 ] @
Batali persiranje!
[ lepi.cane @ 11.10.2009. 23:19 ] @
Citat: Nedeljko: Batali persiranje! Dobro, ako baš insistiraš Šalu na stranu, pokušaću da kompletno rešim zadatak jer mislim da će to sada biti izvodljivo, pa ću sutra postovati rešenje. [ lepi.cane @ 12.10.2009. 22:41 ] @
Dokaz tvrđenja pod e)
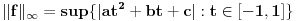 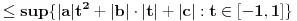 , , a kako 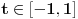 onda je onda je 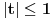 , pa je prethodni izraz , pa je prethodni izraz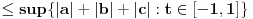 kako 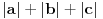 ne zavisi od ne zavisi od  ,to je prethodni izraz ,to je prethodni izraz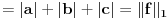 Na osnovu ovoga zaključujemo da je: 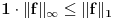 odnosno odnosno 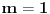 Za dokaz drugog dela nejednakosti koristimo se Nedeljkovom opservacijom da je: 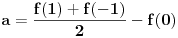 ; ; 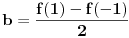 i i 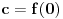 Sada imamo da je: 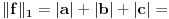 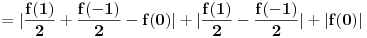 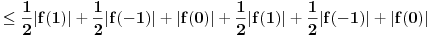 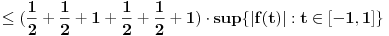 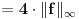 , odnosno , odnosno 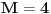 Ovim smo pokazali da je 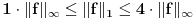 Molim cenjene posetioce podforuma matematika da pogledaju ovaj pokušaj dokaza, i da ukažu na eventualne greške. Takođe, ako neko ima bolju ocenu za  , tj. ako ima dokaz da postoji , tj. ako ima dokaz da postoji 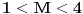 , neka postuje. Hvala. , neka postuje. Hvala.[ lepi.cane @ 13.10.2009. 00:35 ] @
Dokaz tvrđenja pod g)
Uočimo skup 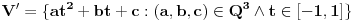 Može se relativno lako pokazati da je 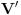 prebrojiv. prebrojiv. Dokazaćemo da je 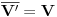 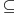 Evidentno je da je 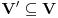 , a pošto je V zatvoren skup, onda važi , a pošto je V zatvoren skup, onda važi 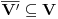 . . Ovo je zbog osobine adherencije da je to najmanji zatvoren skup koji sadrži 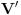 kao podskup. kao podskup.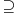 Uočimo proizvoljnu funkciju 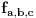 iz iz  . .Poznato je da postoje nizovi racionalnih brojeva 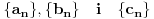 takvi da je takvi da je 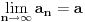 , , 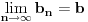 i i 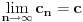 Pokazano je, takođe da je funkcija 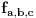 granica niza granica niza 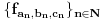 , a to znači da u svakom otvorenom skupu , a to znači da u svakom otvorenom skupu koji sadrži 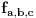 ima i elemenata iz ima i elemenata iz 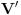 , što znači: , što znači: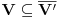 Pokazali smo da je 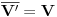 , tj , tj 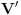 je prebrojiv gust podskup od je prebrojiv gust podskup od  . .Primedba: Kako su sve norme na konačno-dimenzionom skupu ekvivalentne, a to tvrđenje se sada može koristiti jer se pod f) ovog zadatka lako dokazuje da je V konačno-dimenzioni prostor dimenzije 3, u drugom delu tvrđenja nije naznačeno o kojoj se normi radi, jer niz 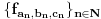 konvergira za bilo koju normu. konvergira za bilo koju normu.[ Nedeljko @ 13.10.2009. 05:42 ] @
[ lepi.cane @ 13.10.2009. 17:43 ] @
Citat: Nedeljko: Ma, u redu je s tim što ne vidim gde je pokazano da niz 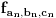 konvergira ka konvergira ka 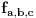 . Može preko ekvivalentnosti normi, s tim da se onda dokaže konvergencija u bar jednoj. . Može preko ekvivalentnosti normi, s tim da se onda dokaže konvergencija u bar jednoj.Može ovako: 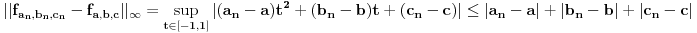 . .Naravno, samo sam bio ubeđen da sam konvergenciju dokazao u nekom od prethodnih postova, ali dokaz je bio za konvergenciju Košijevog niza, odnosno kompletnost prostora V [ lepi.cane @ 14.10.2009. 00:03 ] @
Što se tiče poslednje stavke, prilično jednostavno se dokazuje da je preslikavanje A linearno i neprekidno, ali da mu odredim normu, e tu sam se stvarno zakucao, ili ne vidim drveće od šume.
Jasno se vidi da je 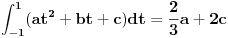 Ako normu linearnog preslikavanja definišemo kao: 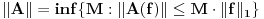 , odnosno kao , odnosno kao 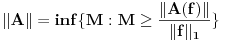 , ,dobijamo da je 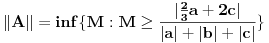 , s čim ne znam šta da počnem. , s čim ne znam šta da počnem.Ako, pak, normu linearnog preslikavanja dafinišemo kao: 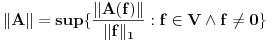 , , dobijamo da je 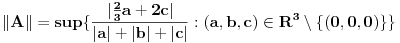 , , s čim takođe ne znam šta ću. I, konačno, ako normu definišemo kao: 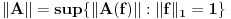 , dobijamo da je: , dobijamo da je: 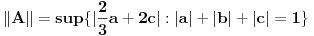 , , što mi opet ništa ne pomaže. Dakle, ponestalo mi ideja. Pomagajte! [ lepi.cane @ 14.10.2009. 17:49 ] @
[ Nedeljko @ 14.10.2009. 18:21 ] @
[ lepi.cane @ 14.10.2009. 18:52 ] @
Ja sam to razumeo na sledeći način:
Norma preslikavanja A je 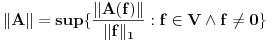 . .Ti si dokazao da je 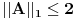 , a u isto vreme da postoje vrednosti za a, b i c za koje važi jednakost. , a u isto vreme da postoje vrednosti za a, b i c za koje važi jednakost.Na osnovu toga možemo zaključiti da je 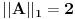 . .Jel' to to? Ako jeste, prelazim na novi zadatak. [Ovu poruku je menjao lepi.cane dana 14.10.2009. u 20:48 GMT+1] [ Nedeljko @ 14.10.2009. 20:00 ] @
Jeste, samo što sam hteo da ti pokažem kako se dobijaju konstante a,b,c za koje se dostiže jednakost.
[ lepi.cane @ 14.10.2009. 20:35 ] @
Razbra', hvala, idem na drugi zadatak.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|