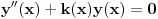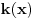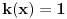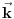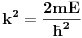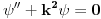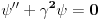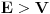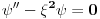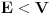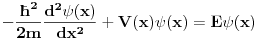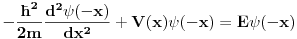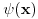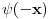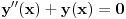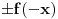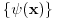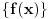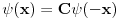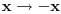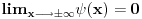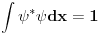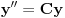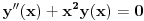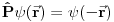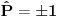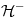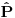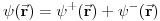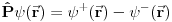[ Nemanjich @ 14.10.2009. 18:05 ] @
|
| Moze li mi neko reci da li su navedene teoreme tacne?
Ako funkciju koja je parna(neparna) podelimo funkcijom koja nije ni parna ni neparna dobijamo funkciju koja nije ni parna ni neparna.
Ako funkciju koja nije parna niti neparna podelimo funkcijom koja nije ni parna ni neparna dobijamo funkciju koja nije ni parna ni neparna.
Ja sam pokusao nesto kao da ih dokazem i cini mi se da su tacne, ali ipak bih voleo da mi neko malo upuceniji kaze da li su tacne ili ne.
Hvala! |
[ Nedeljko @ 14.10.2009. 18:33 ] @
Prvo je tačno. Što se drugog tiče, podeli bilo koju funkciju, koja nikada nije jednaka nuli samom sobom i dobićeš nenula konstantu, koja je svakako parna funkcija. Hoću reći da drugi deo nije tačan.
[ Nemanjich @ 14.10.2009. 18:47 ] @
Hvala Nedeljko, a ako bih preformulisao drugu teoremu: kolicnik dve razlicite funkcije koje nisu ni parne ni neparne, ne moze biti ni parna ni neparna funkcija?
Cini mi se da ni ovo nije tacno(npr slucaj ako se mogu skratiti delovi funkcija koji ih cine da nisu ni parne ni neparne).
Resavam problem k(x)=-y''(x)/y(x), gde je k(x) parna funkcija , pa treba da dokazem da y(x) moze biti samo parna ili neparna funkcija.
[Ovu poruku je menjao Nemanjich dana 14.10.2009. u 19:58 GMT+1]
[Ovu poruku je menjao Nemanjich dana 14.10.2009. u 19:59 GMT+1]
[Ovu poruku je menjao Nemanjich dana 14.10.2009. u 20:32 GMT+1]
[ Nedeljko @ 14.10.2009. 18:52 ] @
Hajde, razmisli malo. Nije teško.
[ Nemanjich @ 14.10.2009. 19:05 ] @
mislis da razmislim u vezi one preformulisane teoreme ili problema?
(editovao sam jedan post, a nisam video da si odgovorio pa sam se malko zbunio)
[ Nedeljko @ 14.10.2009. 19:57 ] @
Jednačina 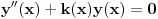 , gde je 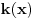 parna funkcija, može imati rešenja koja nisu ni parna ni neparna. Uzmi recimo da je 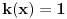 . [ Nemanjich @ 14.10.2009. 20:16 ] @
Evo da ne idem unaokolo:
Na casu iz osnova fizicke elektronike dobili smo neobavezni domaci da dokazemo da su za simetricni(parni) potencijal moguce samo talasne funkcije cestice koje su ili parne ili neparne.
Pa sad kada se to sve stavi u Sredingerovu jednacinu, kaze da je k(x)=2m(E-U(x))/(ħħ) dobijemo j-nu y''(x)+k(x)y=0. I ja se sa time sada ''igram'' .
Ne znam mozda oni to nisu lepo formulisali.
[ petarm @ 15.10.2009. 18:52 ] @
Pogledaj kako je definisano  ? Pogresio si u prethodnom postu! [ Nemanjich @ 15.10.2009. 19:26 ] @
Petre, ne razumem gde sam pogresio. Mozda prosto ne vidim, mozda je neki nesporazum ili nesto trece. Ako hocu da uz y'' stoji samo 1, onda pomnozim izraz sa -2m/(ħħ), i onda mi uz y stoji 2m(E-U(x))/(ħħ), za koje kazem da je k(x), koje zadovoljava uslov k(-x)=k(x), jer je U(-x)=U(x).
Izvini sto gnjavim, ali hajd' reci gde sam pogresio.
[ petarm @ 16.10.2009. 22:22 ] @
U fizici je 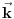 talasni vektor, a 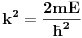 . Tako da tvoja oznaka unosi zabunu.
Za slobodnu česticu Šredingerova jednačina će imati formu
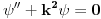
Ako je potencijal (odomaćen naziv za potencijalnu energiju) konstantna Šredingerova jednačina će imati formu
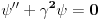 , ako je 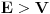
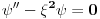 , ako je 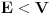
Nemoj zapisivati jednačinu u obliku u kojem jesi. Već razmatraj sledeće
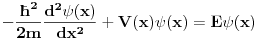
i
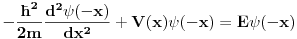
I 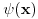 i 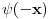 zadovoljavaju istu ODJ. Šta zaklučuješ odatle? Prodiskutuj ovo? [ Nedeljko @ 16.10.2009. 22:51 ] @
Citat: petarm: I 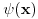 i 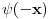 zadovoljavaju istu ODJ. Šta zaklučuješ odatle?
Odatle ne sledi da je svako rešenje ili parna ili neparna funkcija.
ODJ 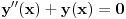 ima skup rešenja sa osobinom da ako mu pripada  , pripadaju mu i 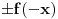 , ali među rešemnjima ima funkcija koje nisu ni parne, ni neparne. [ petarm @ 16.10.2009. 23:05 ] @
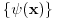 nisu ma kakve funkcije 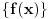 . Ona zadovoljavaju neke uslove koji su Nemanjich-u pretpostavljam poznati. Pa čekamo njegov odgovor! :) [ Nedeljko @ 17.10.2009. 00:40 ] @
Ne znam koji su to dodatni uslovi, ali ona argumentacija ne drži vodu. Možda uz to i još nešto može da se izvede željeni zaključak.
Da li bi mogao ovde da napišeš te uslove?
[ Nemanjich @ 17.10.2009. 05:40 ] @
Jeste, trebao sam nekim drugim slovom da oznacim onu gornju vrednost(ali sam ga lepo definisao, tacno se znalo na sta se odnosi. Fizicka velicina nije zavisna od slova oznacavanja). talasna f-ja treba da zadovolji uslove konacnosti, jednoznacnosti, neprekidnosti, diferencijabilnosti (osim cini mi se ako je cestica u beskonacno dubokoj jami) i na kraju normiranosti (nismo ucili kako se normira slobodna cestica, to tek narednog semestra u KM).
Za "neslobodnu" cesticu za x->∞ tada y->0 (Ipak treba napisati preko integrala normiranost).
Meni je u pocetku bila ideja da resim SJ za parni potencijal, i odatle vidim da je talasna f-ja ili parna ili neparna (mislio sam da ce to biti u zavisnosti od razlike U-E). Videh da tako ne moze. Posle toga mislio sam da napisem SJ za x i -x, pa kako je U(x)=U(-x), izjednacim j-ne i dobijem fin uslov koji je zadovoljen za parnu ili neparnu talasnu f-ju, a nikako nisam uspeo da dokazem da ne vazi za f-ju koja nije ni parna ni neparna.
Sada cu videti ovo (sto sam cini mi se probao, ali nisam znao gde da primenim osobine talasne f-je).
Hvala.
[Ovu poruku je menjao Nemanjich dana 17.10.2009. u 07:54 GMT+1]
[ Nemanjich @ 17.10.2009. 07:03 ] @
Za sada dobijem da je Ψ(x)=CΨ(-x), gde je CC*=1
Ali cini mi se da nema sanse da uspem da dokazem da je C iz R. (mada mozda i ima).
[Ovu poruku je menjao Nemanjich dana 17.10.2009. u 08:15 GMT+1]
[ Nemanjich @ 17.10.2009. 07:21 ] @
Mozda sam pogresio negde u racunu.
(Ovde sam vec bio dosao do uslova Ψ(-x)Ψ''(x)-Ψ(x)Ψ''(-x)=0, da li je tacno napisati (Ψ(-x)Ψ'(x)-Ψ(x)Ψ'(-x))' =0 ? Mislim da je to OK(posto se izvod Ψ(-x), radi kao izvod slozene f-je), al' cisto da pitam).
[Ovu poruku je menjao Nemanjich dana 17.10.2009. u 08:35 GMT+1]
[ petarm @ 17.10.2009. 09:18 ] @
Da možeš to koristiti! Pogledaj ovu temu
http://www.elitesecurity.org/t329971-0[ petarm @ 17.10.2009. 09:23 ] @
U slučaju kontinualnog spektra vrši se "normiranje" na  funkciju. Ali to su zaista nefizički slučajevi. [ petarm @ 17.10.2009. 09:52 ] @
Citat: Nemanjich: Za sada dobijem da je Ψ(x)=CΨ(-x), gde je CC*=1
Ali cini mi se da nema sanse da uspem da dokazem da je C iz R. (mada mozda i ima).
[Ovu poruku je menjao Nemanjich dana 17.10.2009. u 08:15 GMT+1]
Ako si došao do 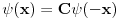 , šta se dešava pri inverziji 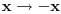 ? [ Nedeljko @ 17.10.2009. 09:57 ] @
Može li neko da da matematičku formulaciju tih dodatnih uslova, pa da i ja malo pratim.
[ petarm @ 17.10.2009. 10:09 ] @
Razmatramo vezana stanja. To znači:
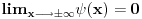
Fja stanja mora biti diferencijabilna. Ona je element  prostora.
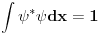 integral po celom prostoru
Ovo se baš normira na jedinicu da bi taj integral imao smisao verovatnoće nalaženja čestice, a  - gustine verovatnoće
Zato za gotovo sve potrebe u kvantnoj koristimo ortonormiran skup stanja. [ Nemanjich @ 17.10.2009. 11:27 ] @
heeehehehehhe, stvarno jeste to, jako jednostavna ideja za zamenu -x u x,a ne bih je se setio sigurno jos par sati. :)))))
Hvala puno Petre i Nedeljko!!!!!
[ petarm @ 17.10.2009. 11:30 ] @
Nema na čemu!  [ Nemanjich @ 19.11.2009. 08:39 ] @
Da vas pitam nesto u vezi ovoga:
za j-nu:
y''(x)+k(x)y(x)=0 (gde je k(x) parna funkcija (za divno cudo :) ))
Da li sam ja ovde mogao odmah da pretpostavim da postoji funkcija y(x) zadovoljava uslov y(-x)=Cy(x) (hocu reci da ne mora svaka da zadovolji, vec postoji neka koja zadovoljava taj uslov) .
Posto onda vazi:
y''(-x)/C+k(x)y(-x)/C=0
y''(-x)/C+k(-x)y(-x)/C=0
y''(-x)+k(-x)y(-x)=0, odakle je:
y''(x)+k(x)y(x)=0
?
[Ovu poruku je menjao Nemanjich dana 19.11.2009. u 10:49 GMT+1]
[ Nedeljko @ 19.11.2009. 12:31 ] @
Ne.
Uzmi da ke k(x)=1. To je svakako parna funkcija kao konstanta. Međutim, sinus je jedno od rešenja, a sinus nije parna funkcija.
Ovo samo znači da ako je y(x) rešenje, onda je i y(-x) rešenje.
[ Nemanjich @ 19.11.2009. 18:36 ] @
"Međutim, sinus je jedno od rešenja, a sinus nije parna funkcija." - ovde mi nije bas jasno sta si hteo da kazes.
Pa dobro, ja nisam ni rekao da resenje mora da bude strogo parna funkcija, vec samo da postoji klasa resenja koja ima osobinu y(-x)=Cy(x), gde spadaju i neparna resenja.
[ Nedeljko @ 19.11.2009. 21:41 ] @
Rešenja jednačine 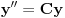 su (u zavisnosti od konstante C)
1. Linearni polinomi,
2. Linearne kombinacije sinusa i kosinusa od ugla pomnoženog istom konstantom
3. Linearne kombinacije hiperboličkog sinusa i hiperboličkog kosinusa, od argumenta pomnoženog istom konstantom.
Od svega toga, jednačinu 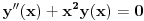 zadovoljava samo nula funkcija. [ NicholasMetropolis @ 19.11.2009. 23:07 ] @
Citat: Nemanjich:
Evo da ne idem unaokolo:
Na casu iz osnova fizicke elektronike dobili smo neobavezni domaci da dokazemo da su za simetricni(parni) potencijal moguce samo talasne funkcije cestice koje su ili parne ili neparne.
Pa sad kada se to sve stavi u Sredingerovu jednacinu, kaze da je k(x)=2m(E-U(x))/(ħħ) dobijemo j-nu y''(x)+k(x)y=0. I ja se sa time sada ''igram'' .
Ne znam mozda oni to nisu lepo formulisali. .
Ne moraš da se bakćeš sa parnim i neparnim funkcijama.
Neka je operator prostorne inverzije definisan u koordinatnoj reprezentaciji dejstvom na talasnu f-ju
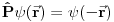
Dvostruka inverzija sve vraća na početak pa mora da važi

iz čega sledi da je
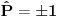
Dakle, dejstvo operatora prostorne inverzije deli prostor stanja  na dva potprostora stanja  i 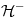 .  čine stanja na koja 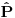 deluje kao 1 (parna stanja), dok 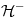 čine stanja na koja 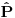 deluje kao -1 (neparna stanja).
Pogledajmo sada stanje koje je linearna kombinacija parnog i neparnog stanja
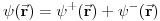
Ako delujemo sa 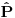 na ovo stanje imamo
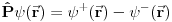
Dakle, dobijamo stanje koje je nekolinearno sa početnim te i fizički različito od njega. Ako je potencijal simetričan u odnosu na prostornu inverziju, operator prostorne inverzije ne sme dejstvom na stanja da proizvede fizički različito stanje (budući da je prostorna inverzija simetrija sistema) tako da su stanja koja su linearna kombinacija stanja iz  i 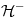 nedozvoljena što znači da stanja mogu biti samo ili parna ili neparna. [ Nemanjich @ 20.11.2009. 07:09 ] @
@ Nedeljko
Hvala Nedeljko, ali:
Ako tu jednacinu zadovoljava samo nula funkcija, za nju svakako vazi: y(-x)=Cy(x), posto je y(x)=0 za svako x tada C moze uzimati sve moguce vrednosti,
(Cini mi se kao da ima neki nesporazum izmedju nas dvojce), mene ne interesuje opste resenje jednacine, vec samo neka partikularna koja zadovoljavaju jednacinu, a imaju osobinu y(-x)=Cy(x).
@ NicholasMetropolis
Hvala, skontao sam sta si napisao.
Uspeo sam ja da dokazem teoremu pod pretpostavkom da postoji funkcija koja je parna i zadovoljava jednacinu i pod pretpostavkom da postoji funkcija koja je neparna i zadovoljava jednacinu, bez ukidanja mogucnosti da postoje neke druge funkcije. Ja sam sada samo hteo da vidim da li mi je pocetna pretpostavka tacna (odnosno da li vazi da parna i neparna funkcija zadovoljava jednacinu y''(x)+k(x)y(x)=0 ).
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|