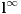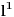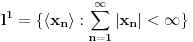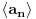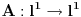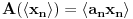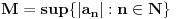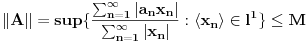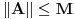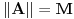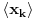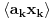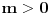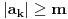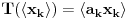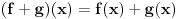[ lepi.cane @ 16.10.2009. 21:39 ] @
|
[ Nedeljko @ 16.10.2009. 22:00 ] @
Dakle,
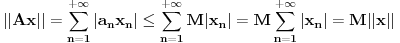 . .Da bi važila jednakost, potrebno je i dovoljno da na svim mestima važi znak jednakosti, tj. da je 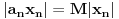 , što je tačno u slučaju kada je , što je tačno u slučaju kada je 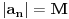 ili ili 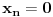 . Dakle, ne bi bilo loše da to važi za svako . Dakle, ne bi bilo loše da to važi za svako  . .To je sa nenula vektorom moguće ako postoji bar jedno  takvo da je takvo da je 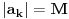 . Tada za vektor . Tada za vektor 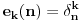 važi važi 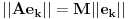 . .No, ti nemaš pretpostavku da postoji takvo  , već samo da je , već samo da je 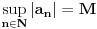 . Zato ovo rešenje ne prolazi u opštem slučaju, ali ideja je blizu. . Zato ovo rešenje ne prolazi u opštem slučaju, ali ideja je blizu.Ako već ne možeš da nađeš  takvo da je takvo da je 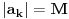 , onda za ma koje , onda za ma koje  postoji postoji  takvo da je takvo da je 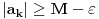 . No, tada je . No, tada je 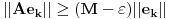 , odakle sledi tvrđenje. , odakle sledi tvrđenje.[ lepi.cane @ 16.10.2009. 22:06 ] @
Hvala, shvatio!!!
[ lepi.cane @ 17.10.2009. 15:09 ] @
Nastavak ovog zadatka glasi:
Uz prethodno dogovorene oznake dokazati da ako za neki niz 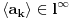 važi da važi da 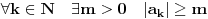 onda je preslikavanje onda je preslikavanje 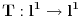 dato sa dato sa 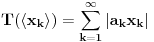 , bijekcija. , bijekcija.Moja primedba je sledeća: Uočimo niz 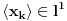 i neka je niz i neka je niz 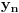 takav da takav da 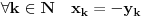 Tada je 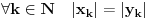 i važi da je i važi da je 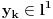 Zaključujemo 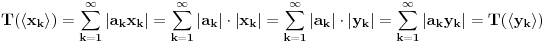 Pronašli smo dva niza 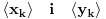 takvi da takvi da 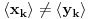 , a za koje važi , a za koje važi 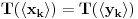 . .Dakle T nije 1-1, dakle nije bijekcija. Ko je pogrešio, ja ili onaj ko je postavio zadatak? [ Nedeljko @ 17.10.2009. 15:26 ] @
[ lepi.cane @ 17.10.2009. 16:21 ] @
[ lepi.cane @ 22.10.2009. 19:24 ] @
Da ne postavljam novu temu, evo još jednog iz edicije "funkcionalna analiza".
Neka je 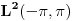 skup neprekidnih funkcija skup neprekidnih funkcija 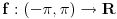 , takvih da važi , takvih da važi 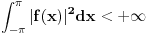 Dokazati da je 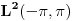 vektorski prostor nad vektorski prostor nad 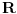 E, sad, ima ovaj zadatak još "podzadataka", ali ovo je odmah na početku, a potpuno sam ga citirao, dakle nigde nije navedeno u odnosu na koju grupu, pa sad ja bajam u pasulj da li je u odnosu na 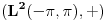 ili na ili na 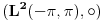 , mada više sam mišljenja da je ova prva. Međutim to je problem, da li funkcija iz , mada više sam mišljenja da je ova prva. Međutim to je problem, da li funkcija iz 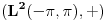 ima inverznu koja je iz tog skupa. Primera radi, funkcija ima inverznu koja je iz tog skupa. Primera radi, funkcija 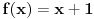 je iz je iz 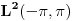 , ali njena inverzna mora biti , ali njena inverzna mora biti 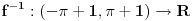 , ili ja to opet nisam skapirao baš najbolje. , ili ja to opet nisam skapirao baš najbolje.[ Cabo @ 22.10.2009. 19:51 ] @
Citat: lepi.cane: E, sad, ima ovaj zadatak još "podzadataka", ali ovo je odmah na početku, a potpuno sam ga citirao, dakle nigde nije navedeno u odnosu na koju grupu, pa sad ja bajam u pasulj da li je u odnosu na 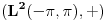 ili na ili na 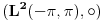 , mada više sam mišljenja da je ova prva. Međutim to je problem, da li funkcija iz , mada više sam mišljenja da je ova prva. Međutim to je problem, da li funkcija iz 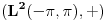 ima inverznu koja je iz tog skupa. Primera radi, funkcija ima inverznu koja je iz tog skupa. Primera radi, funkcija 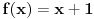 je iz je iz 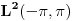 , ali njena inverzna mora biti , ali njena inverzna mora biti 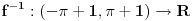 , ili ja to opet nisam skapirao baš najbolje. , ili ja to opet nisam skapirao baš najbolje.Prvo, jedna ograda: nemam blage veze sa Realnim i kompleksnim funkcijama, pa ni sa funkcionalnom analizom, ali ako je ono 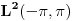 skup funkcija koje slikaju skup funkcija koje slikaju 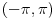 na samog sebe, onda i inverzna funkcija mora pripadati tom skupu. Ako ne, onda se verovatno posmatraju restrikcije na na samog sebe, onda i inverzna funkcija mora pripadati tom skupu. Ako ne, onda se verovatno posmatraju restrikcije na 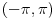 . .[ lepi.cane @ 22.10.2009. 20:41 ] @
[ Cabo @ 22.10.2009. 20:57 ] @
[ lepi.cane @ 22.10.2009. 21:10 ] @
Ovo je primer ispitnog zadatka, tako da nije ni iz kakve knjige. Drugo, upravo i kažem da bajam u pasulj već izvesno vreme, da shvatim šta su inverzi dotičnih funkcija. Ostalo sve štima, ali me ovo buni. Prilično sam uveren da je problem do mene, jer piše "dokazati da je", a ne "ispitati da li je".
[ Nedeljko @ 23.10.2009. 07:20 ] @
[ lepi.cane @ 23.10.2009. 14:43 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|