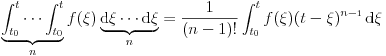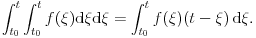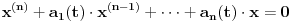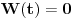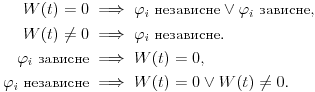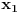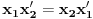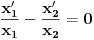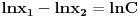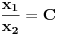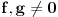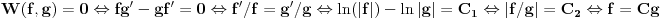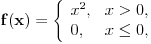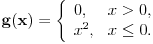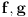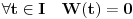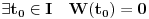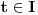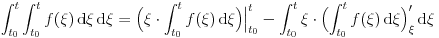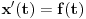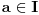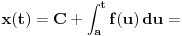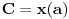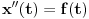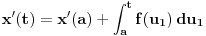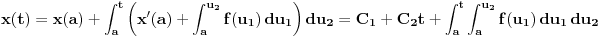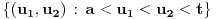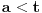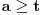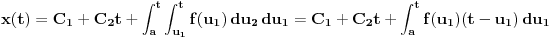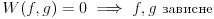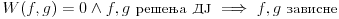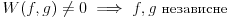[ Cabo @ 24.10.2009. 17:17 ] @
|
[ Cabo @ 24.10.2009. 18:34 ] @
Citat: Fact Given two functions  and and 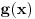 that are differentiable on some interval that are differentiable on some interval  . .(1) If 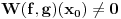 for some for some  in in  , then , then  and and 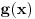 are linearly independent on the interval are linearly independent on the interval  . .(2) If  and and 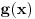 are linearly dependent on are linearly dependent on  then then  for all for all  in the interval in the interval  . .Be very careful with this fact. It DOES NOT say that if  then then  and and 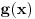 are linearly dependent! In fact it is possible for two linearly independent functions to have a zero Wronskian! are linearly dependent! In fact it is possible for two linearly independent functions to have a zero Wronskian!Pogledaj i moju prethodnu poruku. Dopunio sam poslednji deo (mali problemi sa 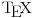 -om). -om).A čekam i odgovor na prvo pitanje. [ Cabo @ 24.10.2009. 19:14 ] @
Sad sam probao ovo:
Neka su  i i  dve linearno nezavisne funkcije. Dakle, ako je dve linearno nezavisne funkcije. Dakle, ako je 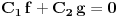 onda je onda je 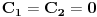 . .Neka je vronskijan nula: 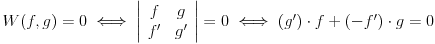 , pa mora biti , pa mora biti 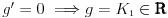 i i 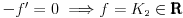 . Odatle je za . Odatle je za 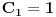 i i 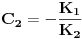 ( (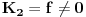 ) ispunjeno ) ispunjeno 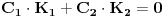 , a , a 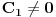 i i 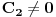 . .Ali zašto bi se čovek onda toliko trudio da napomene ono što je napomenuo?! o_O Po njegovom, 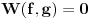 nam ne govori ništa. ?_? nam ne govori ništa. ?_?[Ovu poruku je menjao Cabo dana 24.10.2009. u 21:02 GMT+1] [Ovu poruku je menjao Cabo dana 24.10.2009. u 21:19 GMT+1] [ Cabo @ 24.10.2009. 20:26 ] @
[ Nedeljko @ 24.10.2009. 20:53 ] @
[ Nedeljko @ 24.10.2009. 20:59 ] @
[ Cabo @ 24.10.2009. 21:20 ] @
[ Nedeljko @ 24.10.2009. 22:26 ] @
Molim? Kakvo je to pitanje? Šta ti očekuješ od Julkine knjige? Sećam se kada je preko skupa nula rešenaj dif. j-ne dokazivala da su funkcije A*sin(t) i B*sin(t) linearno nezavisne. Posle je popravila to, a dodala druge "bisere".
Šalu na stranu, nećeš naći dif. j-nu oblika y''(x)=u(x,y(x),y'(x)), gde je f-ja u neprekidno diferencijabilna po trećem argumentu, a čija su rešenja funkcije f i g. Štaviše, f i g nemaju drugi izvod u tački 0. Satim nećeš naći ni odgovarajuću linearnu dif. j-nu drugog reda kakvu zahteva ta teorema. Mogu se napakovati primeri sa beskonačno diferencijabilnim funkcijama (zameni  sa sa 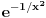 ), ali će koordinatni početak biti singularna tačka eventualne dif. j-ne. Ne odnosi se to na linearnu nezavisnost bilo kakvog sistema funkcija, već taj sistem funkcija mora biti rešenje iste linearne diferencijalne jednačine. ), ali će koordinatni početak biti singularna tačka eventualne dif. j-ne. Ne odnosi se to na linearnu nezavisnost bilo kakvog sistema funkcija, već taj sistem funkcija mora biti rešenje iste linearne diferencijalne jednačine.[ petarm @ 25.10.2009. 00:00 ] @
Citat: Citat: Nedeljko je ovde lepo dodao uslov! Tako je za nenula funkcije! Mada za takve prakticno uvek i definisemo Jakobijan. Citat: Nedeljko: Iskren da budem, zapis 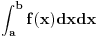 mi nije jasan. Jasno je meni da je to integracija u ravni, ali daj napiši indekse promenljivih. Ne može ovako. mi nije jasan. Jasno je meni da je to integracija u ravni, ali daj napiši indekse promenljivih. Ne može ovako.Tacnije 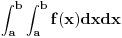 . Da i meni nije jasan taj zapis. A problem je sto . Da i meni nije jasan taj zapis. A problem je sto 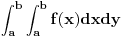 ne daje gornji rezultat. ne daje gornji rezultat. [ Cabo @ 25.10.2009. 17:40 ] @
Citat: Nedeljko: Molim? Kakvo je to pitanje? Šta ti očekuješ od Julkine knjige? Očekujem da položim ispit. Izgleda da će morati da radi „bubanje“. Citat: petarm: Da i meni nije jasan taj zapis. A problem je sto 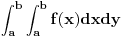 ne daje gornji rezultat. ne daje gornji rezultat.Ja sam potpuno zbunjen time kako je 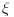 moglo da bude rezultat integracije po moglo da bude rezultat integracije po 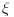 u granicama od u granicama od 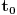 do do  . :-/ . :-/[ miki069 @ 26.10.2009. 01:58 ] @
Probaj onaj suludi "dvostruki integral" da uradiš parcijalnom integracijom gde ti je:
dV = d(epsilon) odakle je V=epsilon a U= unutrašnjem integralu od (f(epsilon)*d(epsilon)) odakle je dU = f(epsilon)*d(epsilon). Posle zamena granica se dobija trvđenje ali uz jedan "čudan" korak oko menjanja granica u prvom članu rešenja . Aj ispiši ovu parcijalnu integraciju u Tex-u pa da vidimo šta je "smuvano" u finalnom koraku. [ Nedeljko @ 26.10.2009. 15:57 ] @
Izvini, a možeš li da napišeš kontekst, koji će ti andrak ta formula, pa da vidimo?
[ petarm @ 26.10.2009. 18:08 ] @
Citat: miki069: Probaj onaj suludi "dvostruki integral" da uradiš parcijalnom integracijom gde ti je: dV = d(epsilon) odakle je V=epsilon a U= unutrašnjem integralu od (f(epsilon)*d(epsilon)) odakle je dU = f(epsilon)*d(epsilon). Posle zamena granica se dobija trvđenje ali uz jedan "čudan" korak oko menjanja granica u prvom članu rešenja . Aj ispiši ovu parcijalnu integraciju u Tex-u pa da vidimo šta je "smuvano" u finalnom koraku. Mozemo izmisliti neki metod pa dobiti gornji rezultat, ali cemo ga ipak morati opravdati! Meni stvarno takav zapis nije jasan. 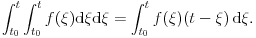 [ Nedeljko @ 26.10.2009. 19:20 ] @
Nije reč ni o pravdanju, već o razumevanju značenja zapisa.
[ Cabo @ 26.10.2009. 20:23 ] @
Citat: Nedeljko: Izvini, a možeš li da napišeš kontekst, koji će ti andrak ta formula, pa da vidimo? Rekoh već, snižavanje reda DJ. *uzdah* U redu, evo: a) Razmotrimo jednačinu oblika 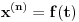 (2.2.1), gde je (2.2.1), gde je 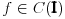 . Saglasno teoremi 2.1.1, oblast egzistencije i jedinstvenosti rešenja ove jednačine je . Saglasno teoremi 2.1.1, oblast egzistencije i jedinstvenosti rešenja ove jednačine je 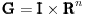 . Integraleći jednakost (2.2.1) . Integraleći jednakost (2.2.1)  puta dobijamo opšte rešenje u oblasti puta dobijamo opšte rešenje u oblasti 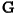 : :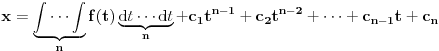 , gde su , gde su 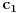 , ,  , , 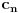 proizvoljne konstante. Rešenje proizvoljne konstante. Rešenje 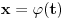 koje zadovoljava početne uslove koje zadovoljava početne uslove 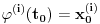 , ,  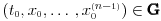 je funkcija je funkcija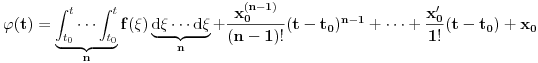 . .Kako je 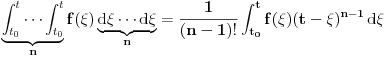 , ,to je 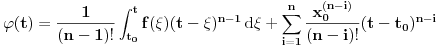 . .Bolje? [Ovu poruku je menjao Cabo dana 26.10.2009. u 21:36 GMT+1] [ Nedeljko @ 27.10.2009. 07:21 ] @
[ Nedeljko @ 27.10.2009. 07:40 ] @
[ Cabo @ 27.10.2009. 18:53 ] @
Hvala puno!
Imaš čokoladu od mene. Pitam se još da li su tačni i dokazi u kojima zaključuje da je neka funkcija nula tako što kaže da su u oblasti egzistencije i jedinstvenosti sva rešenja jednaka, a trivijalno rešenje zadovoljava DJ. [Ovu poruku je menjao Cabo dana 27.10.2009. u 20:05 GMT+1] [ petarm @ 28.10.2009. 10:38 ] @
Ajd kad se vec prica o tome? Sta mislite o ovom delu iz integralnih jednacina? Iste autorke! Knjiga diferencijalne jednacine 2, ako se ne varam?
[ Nedeljko @ 28.10.2009. 10:46 ] @
Ako 0 zadovoljava Košijev zadatka u oblasti egzistencije i jedinstvenosti rešenja, naravno da je 0 jedino rešenje tog Košijevog zadatka.
Prvu autorkinu knjigu sam čitao preko volje, na moranje, dok drugu nisam i ne želim da čitam. Nego, šta je to presecanje redova? Imaš li neki link? [ Cabo @ 28.10.2009. 10:54 ] @
[ petarm @ 28.10.2009. 12:21 ] @
Citat: Nedeljko: Prvu autorkinu knjigu sam čitao preko volje, na moranje, dok drugu nisam i ne želim da čitam. Ok! Ja cu okaciti ipak jedan deo iz integralnih jednacina. Ako nekoga zanima. Neko je to vec okacio na ovom Forumu. Meni je iskreno koristio ovaj deo jer ima nekih resenih zadataka. A teoriju nisam citao odavde. I provlaci se isti zapis koji je izazvao zabunu u ovoj temi! Citat: Nedeljko: Nego, šta je to presecanje redova? Imaš li neki link? Nemam link! Trudicu se da krajem sledece nedelje otkucam nesto o tome u posebnoj temi pa da se otvori diskusija. Trenutno ne mogu da stignem jer spremam ispit. Pozdrav [ Nedeljko @ 28.10.2009. 12:22 ] @
@Cabo
Pa, to važi u slučaju da su f i g rešenja iste linearne diferencijalne jednačine drugog reda sa neprekidnim koeficijentima. Takođe, to važi u klasi analitičkih funkcija. Ja sam samo dokazao da to ne važi za ma kakve dovoljno glatke funkcije f i g. [ petarm @ 28.10.2009. 12:26 ] @
Evo nadjoh! Imam problem sa uploadom!
http://www.elitesecurity.org/t...-Integralne-jne-zadaci-resenja [Ovu poruku je menjao petarm dana 28.10.2009. u 13:37 GMT+1] [Ovu poruku je menjao petarm dana 28.10.2009. u 13:38 GMT+1] [ Cabo @ 28.10.2009. 17:56 ] @
Citat: Nedeljko: @Cabo Pa, to važi u slučaju da su f i g rešenja iste linearne diferencijalne jednačine drugog reda sa neprekidnim koeficijentima. Takođe, to važi u klasi analitičkih funkcija. Ja sam samo dokazao da to ne važi za ma kakve dovoljno glatke funkcije f i g. U redu. Kako se to onda razlikuje od Dokinsovog slučaja? Da li je razlika samo u neprekidnim koeficijentima? Jer on tvrdi da uz 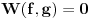 funkcije funkcije  i i  mogu da budu i linearno nezavisne. mogu da budu i linearno nezavisne.DODATAK: A, sad vidim da on uopšte ne pretpostavlja da su funkcije  i i  rešenja DJ. Znači, to je to? rešenja DJ. Znači, to je to?[Ovu poruku je menjao Cabo dana 28.10.2009. u 19:21 GMT+1] [ Nedeljko @ 28.10.2009. 18:55 ] @
Da, to je to.
[ Cabo @ 28.10.2009. 19:23 ] @
[ miki069 @ 28.10.2009. 21:44 ] @
Cabo imaš dokaz kompletan (Teorema3) u skripti prof. dr. Miodraga Petkovća sa Elektroskog fakulteta u Nišu.
Zemi je sa linka http://www.elfak.ni.ac.rs/phpt...avlja/diferencijalne_tekst.pdf Skripta je u celina preslaba za PMF, ali je sažeta i nema bisera. I najbitnije Teorema3. sa dokazom je ono što ti je Nedeljko već razjasnio. Od istog profe imaš skripte i iz nizova, redova, kompleksne analize i verovatnoće i statistike i sve su solidne na linku: http://www.elfak.ni.ac.rs/phptest/new/index.php. Pogotovo verovatnoća i statistika su dobro urađeni. Za zadatke za pismeni ti preporučujem knjigu od prof. Belajčića sa Arhitekture "Diferencijalne jednačine". Nije tip-top za nivo PMF-a ali je postupna, šablonska. Kao Apsen za integrale. Nije puno dokazivao i za usmeni je neupotrebljiva, ali za zadatke za pismeni je izvornik. U fazonu: tip1 (čas1, čas2..), tip2... Kopija Apsena. Imam je. Ako treba javi se. Za teoriju nemam ideju. Osim te "Julke". Ko vam je ta "Julka"??? Jel ima ko knjigu "Zanimljivi matematički problemi" od prof. dr. Miodraga Petkovća??? U bilo kom obliku. Mala (A-5), crvene korice. Imao sam je i neko mi je "pozajmio". Od tada jurim da je kupim, ali je nigde nema. Sad imam samo naslovnu stranu: http://www.miodragpetkovic.com/eng/books/problemi.html [Ovu poruku je menjao miki069 dana 28.10.2009. u 22:55 GMT+1] [ Cabo @ 29.10.2009. 21:33 ] @
Citat: miki069: Cabo imaš dokaz kompletan (Teorema3) u skripti prof. dr. Miodraga Petkovća sa Elektroskog fakulteta u Nišu. Hvala, pogledaću. Citat: miki069: Za zadatke za pismeni ti preporučujem knjigu od prof. Belajčića sa Arhitekture "Diferencijalne jednačine". Nije tip-top za nivo PMF-a ali je postupna, šablonska. Kao Apsen za integrale. Nije puno dokazivao i za usmeni je neupotrebljiva, ali za zadatke za pismeni je izvornik. U fazonu: tip1 (čas1, čas2..), tip2... Kopija Apsena. Imam je. Ako treba javi se. Ma, problem mi je usmeni, lako ću ja zadatke... Citat: miki069: Za teoriju nemam ideju. Osim te "Julke". Ko vam je ta "Julka"??? Interna MATF-ovska stvar. Jedna naša profesorka. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|