Ovo je predmet Numeričke matematike. Funkcija koja predstavlja neke podatke sa određenom tačnošću se zove interpolacioni polinom. Ima ih raznih, Lagranžov je najprostiji i najpoznatiji.

Pogledaj neke knjige iz Numeričke matematike. Matlab je specijalizovan za Numeričku.

Wolfram Mathematica 4.x i novije (do 7.01)
Pročitaj uputstvo, nije baš tako jednostavno korišćenje, odnosno, hoću da kažem da moraš da paziš na sintaksu, ali kad to uklaviriš, vrlo moćan software. Ima, doduše, jednu manu, traže da se plati, ali ...

Nisam siguran da ijedan sw može ovo što on hoće. No, interpolacija je nešto sasvim klasično.

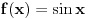
Pa ne može baš dobiti funkciju , ali može recimo neki kubni splajn, ili tako nešto.

Matematiku 7 imam , i boga mi , jeste zeznuta , pogotovo kad treba da se definiše više promenljivih i njihovi međusobni odnosi.

Evo neki Solas je imao sličan problem , samo komplikovaniji . Ja bih rekao da on hoće diferencni oblik jednačine . Može li neka jednostavnija funkcija da se dobije peške (recimo , preko izvoda ili diferencijalnog računa)?

solas:
Pomocu mikrokontrolera pravim termo kontroler koji ce na osnovi izmerene temperature kontrolisati grejace(trijacima) i odrzavati temperaturu vazduha u tunelu konstantnom,
kako sam ja kao i vecina elektronicara uglavnom odsustvovao sa predavanja iz automatike, a istu sam jedva polozi sa 6 a to je jos bilo pre nekoliko godina, slaba vajda da je nesto ostalo u glavi!!!! Secam se ja neceg ali bi mi trebalo jedno 10 dana da prekopam po staroj literaturi pa da se podsetim sta se sve tu radi, a toliko vremena nemam...
E sada ono sto sam ja uspeo da premerim je to da grejaci cija je snaga 1kW(220) pri snazi od 80% (bio je slabiji napon oko 190 kada sam merio) imaju sledecu temperaturnu karakteristiku u zavisnosti od vremena:

pocetna temperatura je bila 17 stepeni. do temperature od 100 stepeni su zagrejali za 16min, do 150 za 37min a do 170 stepeni za 45min. vreme kada je temperatura vidno pocela da se menja je bilo posle 1-1.5 min.

e sada bi ja zamolio nekoga da mi izracuna (simulira u matlabu ili sl) j-nu sa PID regulacijom po kojoj ja treba da kontrolisem ukljucenost grejaca u odredjenom trenutku u zavisnosti od vremena i izmerene temperature.

Znam da nesto bese oblika m[k+1]=Kp*(1+(1/Ti)*(suma(e[k])) + Td*(e[k]-e[k-1])) (m[k+1] mi je valjda duty ratio za sledeci odbirak, e[k] temperatura greske u sadasnjeg odbirka, e[k-1] temperatura greske proslog odbirka a Kp, Ti, Td proporcionalne, integralne i diferencijalne konstante)

E sada kako se podesavaju ovi parametri boga pitaj...a koliko vreme odabiranja da uzmem za ovaj moj sistem, kako da racunam ovo suma(e[k]) kada mi k tezi beskonacno...to je ono sto sam zaboravio...
jel neko mozda ima neki uproscen metod ovog proracuna

znaci funkcija da bude oblika D[k+1]=f(e[k],e[k-1]...), pri cemu je D duty ratio (odnos ukljucenosti grejaca/ perioda PWM-a) pri cemi je D u granicama od 0 do 1 a e[k]=zadataTEMPERATURA - merenaTEMPERATURA, naravno u pitanju je funkcija diskretnog oblika.

Nije bitno da parametri Kp, Ti, Td budu striktno optimalno podeseni, to moze biti po Ziegler Nichols kriterijumu ili nekom drugom...
Ko je radio nesto slicno i zna ovo da proracuna nadam se razume o cemu pricam