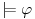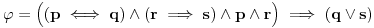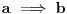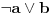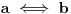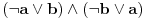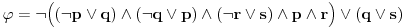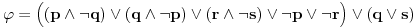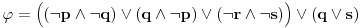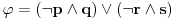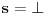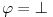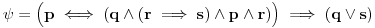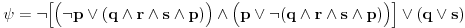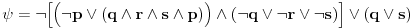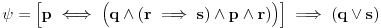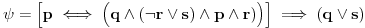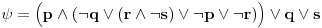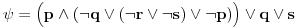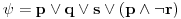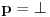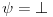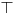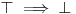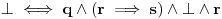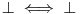[ Man-Wolf @ 24.10.2009. 19:12 ] @
Pozdrav,

Zamolila me je drugarica da joj pomognem oko jednog zadatka iz Tautologije. Naime, malo sam i zaboravio ovo, tako da nisam siguran da li sam dobro uradio zadatak, pa bih zamolio ako neko moze da proveri i da mi kaze da li je dobro. Elem, zadatak je sledeci:

Dokazati da je sledeci iskaz Tautologija (koriscenjem "Metode promenljive" ili "Diskusije po promenljivoj" - nisam siguran kako se zove :S):

Code:


((p <=> q /\ (r => s) /\ p /\ r) => (q \/ s)



Elem, ja sam resio sledecom logikom:

Code:


tau(p) = T



To kad se zameni u zadatku, to izgleda ovako:

Code:


((T <=> q /\ (r => s) /\ T /\ r) => (q \/ s)



Prvo gledam sledecu ekvivalenciju:

Code:

((T <=> q /\ (r => s) /\ T /\ r)


Da bi ona bila tacna, moraju - q, r i s da budu tacni (zbog konjukcije sa desne strane ekvivalencije).

Sada imamo da je cela ta zagrada tacna:

Code:

((T <=> q /\ (r => s) /\ T /\ r) = T


Dalje:

Code:


T => (q \/ s)



Posto smo malopre zakljucili da je "q = T", onda imamo:

Code:


T => (T \/ s)



Posto je u pitanju disjunkcija (u zagradi), sta god da je "s", disjunkcija je Tacna i znaci imamo:

Code:


T => T



I dobili smo da je Tautologija Tacna (ne ?) :-)

E sad, krecemo iz pocetka, sa pretpostavkom da je:

Code:

tau(p) = 0 (ne znam kako se pise znak NETACNO, tako da cu pisati 0 umesto njega)


Zamenom u zadatku, imamo:

Code:

((0 <=> q /\ (r => s) /\ 0 /\ r) => (q \/ s)


Uzimamo i proveravamo levi deo izraza:

Code:

((0 <=> q /\ (r => s) /\ 0 /\ r)


Da bi ekvivalencija bila tacna, moramo sa desne strane izraza da imamo vrednost NETACNO. Posto u konjuckiji sa desne strane ekvivalencije imamo NETACNO (0), odmah znamo da cela implikacija pada i da je vrednost sa desne strane NETACNA. Dobijamo da je ceo prethodni izraz NETACAN.

Zamenom u pocetni zadatak, imamo:

Code:

0 => (q \/ s)


Sta god da imamo sa desne strane implikacije (TACNO ILI NETACNO), izraz ce biti tacan i opet smo dokazali Tautologiju, sto znaci da smo dokazali da je ovaj zadatak tautologija.

Da li sam dobro resio ovo ? :-)

Hvala unapred,

Mihailo Joksimovic
[ Cabo @ 24.10.2009. 19:49 ] @
Pre svega, moraš da malo razgraničiš terminologiju: tautologija je univerzalno istinit iskaz. Činjenica da je iskaz univerzalno istinit se beleži .

Dalje, da li si mislio na ? Ovo nije tautologija.

Proveri. Sastavi tablicu i ispiši sve moguće kombinacije za , , i . Formula je ekvivalentna , a je ekvivalentna , što je .

Izraz postaje:

,
što je ,
tj. ,
i na kraju . Za i se dobija .

A ako si mislio na , to onda postaje:

,

tj. ,


Možda nastavim sledećih dana.

[Ovu poruku je menjao Cabo dana 24.10.2009. u 22:52 GMT+1]
[ Cabo @ 25.10.2009. 17:06 ] @
Evo ovako. Jednačina:


je ekvivalentna sa ,
što je ekvivalentno sa
,
tj. ,
odakle je ,
ili ,
što daje .

Ovo za , , daje .

Dakle, ni ovo nije tautologija. Negde si pogrešio u razmatranju. Proveri tablicom.

Uostalom, zameni vrednosti , , u i dobićeš , ali je , a implikacija je netačna.

[Ovu poruku je menjao Cabo dana 25.10.2009. u 19:39 GMT+1]
[ Cabo @ 25.10.2009. 18:53 ] @
Ah, evo gde je greška:

Citat:
Man-Wolf: 
Code:

((0 <=> q /\ (r => s) /\ 0 /\ r)


Da bi ekvivalencija bila tacna, moramo sa desne strane izraza da imamo vrednost NETACNO. Posto u konjuckiji sa desne strane ekvivalencije imamo NETACNO (0), odmah znamo da cela implikacija pada i da je vrednost sa desne strane NETACNA. Dobijamo da je ceo prethodni izraz NETACAN.


Koja „implikacija“? je ekvivalencija. Ekvivalencija je tačna.