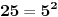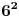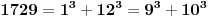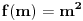Nema tu šta da se razume. Zadatak nema previše smisla.

Šta je poenta skeča? ?_?

resenje je da je jedan imao 24 god. a drugi 25 god. jer je 25=52 i drugi kvadrat 63=36 odnosno za 11 god.pa je on dosao do toga da je 24=4!=4*3*2*1 a 96 +24=120=5!
da li neko ovo moze da razjasni.ovakvo sam nasao objasnjenje!?

Kao što je bilo očekivano, iz rešenja se vidi da zadatak nema nikakvog smisla.

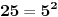
Jedan matematičar je primjetio da drugi ima godina i da ce isti takav rođendan, kvadrat prirodnog broja, imati za 11 godina (imace 36 godina, tj. )!

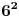
Drugi je primjetio da prvi ima 24=4! godina i da ce isti takav rođendan, faktorijel prirodnog broja, imati za 96 godina (imace 120 godina, tj. 5!)!

Kad smo kod zanimljive matematike, postoji jedna interesantna priča (takođe o dva matematičara) da je Hardi (Godfrey Harold Hardy, 1877-1947) dosao u bolnicu da posjeti Ramanudžana i rekao mu da je došao taksijem 1729, da mu taj broj djeluje sasvim obično i nezanimljivo. Na to je Ramanudžan odgovorio da je to veoma interesantan broj, najmanji koji se može izraziti kao suma dva kuba na dva različita načina, .

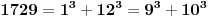
Nadam se da ti je sada jasniji zadatak koji si postavio! Tako ti je to sa matematičarima!

U ovom rješenju imamo faktorijele i kvadrate uzastopnih brojeva. Pitanje je da li je ovo jedino rješenje postavljenog zadatka?

_{[Ovu poruku je menjao Sini82 dana 08.11.2009. u 12:47 GMT+1]}

Samo se potvrđuje da zadatak nema nikakvog smisla.

Moglo je i ovako (vezano za desetični brojni sistem) 2²=4, pa je sledeći "takav" broj 39. Ili 2*5=10, pa je sledeći "takav" 52. Možeš izmisliti koliko hoćeš kriterijuma za "To je takav broj".

Da preformulišemo zadatak tako da ima smisla:

ZADATAK

Odrediti funkcije f:N->N, g:N->N, prirodne brojeve m, n, za koje vrijede jednakosti f(m+1)-f(m)=11, g(n+1)-g(n)=96 i uslovi ograničenja f(m)<=30, g(n)<=30.

RJEŠENJE:

Jedno rješenje je za m=5, g(n)=n! za n=4.

Dakle, prvi matematičar ima f(5)=25 godina a drugi f(4)=24 godine.

NAPOMENA:

Pošto se radi o mladim matematičarima, uvedeni su gore navedeni uslovi ograničenja.

Da li je ovo jedino rješenje postavljenog zadatka?

Izaberimo bilo koje brojeve m,n i a,n<=30. Tada ma koje funkcije f,g:N->N za koje je f(m)=a, f(m+1)=a+11, f(n)=b, f(n)=b+96 zadovoljavaju tražene uslove.

To je rešenje ovog zadatka.

ok.sad je jasnije,veoma sam zadovoljan vasim izlaganjima....