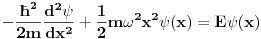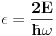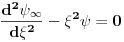[ petarm @ 10.11.2009. 14:00 ] @
|
[ petarm @ 10.11.2009. 14:18 ] @
[ petarm @ 10.11.2009. 14:31 ] @
[ petarm @ 10.11.2009. 14:38 ] @
[ petarm @ 10.11.2009. 14:42 ] @
[ petarm @ 10.11.2009. 14:45 ] @
[ Nedeljko @ 10.11.2009. 14:49 ] @
Nemoj da se ljutiš, ali ja ovde "presecanje redova" vidim samo u naslovu teme. Ni find alatka mi ne pomaže da nađem još mnegde. Lepo je to što si ti rešio Šredingerovu jednačinu, ali šta je tu presecanje redova?
[ petarm @ 10.11.2009. 14:53 ] @
Ili recimo u teoriji diferencnih jednacina uvodi se translacioni operator
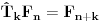 Pa je 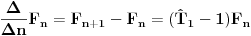 Moze se uvesti i na druge nacine, al ja sam ovako navikao po knjizi "Primena diferencnog racuna u analizi nanostruktura" Bratislava S. Tosica. Npr. kad hocemo da izvrsimo antidiferenciranje funkcije 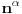 . .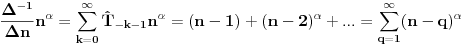 Ovaj red se preseca za 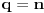 Zbog toga je konacan rezultat antidiferenciranja 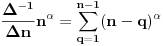 [ petarm @ 10.11.2009. 14:57 ] @
Citat: Nedeljko: Nemoj da se ljutiš, ali ja ovde "presecanje redova" vidim samo u naslovu teme. Ni find alatka mi ne pomaže da nađem još mnegde. Lepo je to što si ti rešio Šredingerovu jednačinu, ali šta je tu presecanje redova? Ne ljutim se pogledaj onaj post gde je dobijena energija! Mislim da ce ti biti jasno na sta mislim! [ Nedeljko @ 10.11.2009. 18:27 ] @
I dalje mi nije jasno šta je od svega ovoga presecanje redova. Znaš li engleski termin, pa da potražim?
[ Nedeljko @ 10.11.2009. 18:32 ] @
I dalje mi nije jasno šta je od svega ovoga presecanje redova. Znaš li engleski termin, pa da potražim?
[ petarm @ 11.11.2009. 15:46 ] @
Citat: Nedeljko: I dalje mi nije jasno šta je od svega ovoga presecanje redova. Citat: 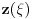 polinom! polinom! 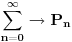 Kako dobiti polinom? 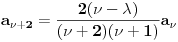 Ako je za neko  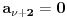 onda su svi visi koeficijenti jednaki nuli, znaci red se preseca! To se desava za onda su svi visi koeficijenti jednaki nuli, znaci red se preseca! To se desava za 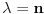 . Onda je resenje polinom stepena . Onda je resenje polinom stepena  . .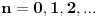 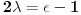 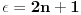 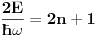 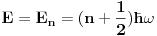 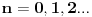 Presecanje reda je uzimanje da su od nekog clana reda svi "visi" clanovi jednaki nuli, odnosno da su koeficijenti uz te stepene jednaki nuli! Bojan Bašić: popravljen citat [Ovu poruku je menjao Bojan Basic dana 11.11.2009. u 18:29 GMT+1] [ Nedeljko @ 11.11.2009. 16:02 ] @
Pa, dobro, imali smo na diferencijalnim jednačinama određivanje polinomskog rešenja linearne diferencijalne jednačine, ako postoji. Ovde si to uradio za redove.
Mogao si samo da napišeš dif j-nu, njeno rešenje u vidu reda i da kažeš "red se preseca na nekom mestu, ako se anulira počev odatle, pa je suma običan polinom" i da to napišeš, pa bi em manje pisao, em bi svima bio jasan. [ petarm @ 11.11.2009. 17:02 ] @
Ovo sam sve ispisao ne bi li neko uzeo i sve procitao! Isao sam polako i dosao do razloga zasto presecamo taj red! Dao sam fizicki razlog za presecanje istog i u tome je lepota svega! A i napisao sam postupak za dobijanje svojstvenih vrednosti energije LHO sto ce nekome u buducnosti koristiti! A iz tog sto bih tebi bio jasan, ne sledi da bih svima bio jasan! A i mnogima ne bi bilo jasno zasto se taj red preseca!
[ Cabo @ 11.11.2009. 20:00 ] @
Citat: petarm: Ovo sam sve ispisao ne bi li neko uzeo i sve procitao! Isao sam polako i dosao do razloga zasto presecamo taj red! Dao sam fizicki razlog za presecanje istog i u tome je lepota svega! A i napisao sam postupak za dobijanje svojstvenih vrednosti energije LHO sto ce nekome u buducnosti koristiti! A iz tog sto bih tebi bio jasan, ne sledi da bih svima bio jasan! A i mnogima ne bi bilo jasno zasto se taj red preseca! Lepota je relativna kategorija. Nekima je lepo ono što je precizno i jezgrovito. Kao, na primer, nama što hoćemo da postanemo matematičari. [ Nedeljko @ 11.11.2009. 20:29 ] @
@petarm
Pa, bio bi jasan da si napisao "presecanje redova je to i to". Ovako, imaš neku priču, koja ima za osnovni cilj da objasni šta je to presecanje redova, a nigde ne kažeš šta je od toga presecanje redova. Na taj način nisi mogao da budeš jasan nikome ko ne zna šta je to do poslednjeg posta, kada si konačno rekao šta je to. Hajde, za tu fizičku priču OK, ali si morao da napišeš šta je tu onaj pojam koji pokušavaš da objasniš. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|