[ Sladjan2S @ 23.11.2009. 18:31 ] @
Pozdrav, studiram na ETF-u, ubrzo imamo kolokvij iz linearne algebre pa sam zapeo na jednom dijelu. Naime, ako imamo funkcije f i g i ako su one NA, tj. surjekcija, onda je i f kompozicija g surjekcija. Takođe, ako su te dvije funkcije bijekcija, njihova kompozicija je bijekcija. Ako nije problem da mi neko malo pomogne kako se to rješava? Ideja, uputstvo, primjer, šta god mi može pomoći. Što se tiče injekcije, shvatio sam kako se dokazuje, a našao sam i temu koja mi je to potvrdila, ali mi je ovo dvoje ostalo nejasno.

Hvala unaprijed.
[ petarm @ 23.11.2009. 20:14 ] @
Probaj dokaz kontrapozicijom. Pretpostavi da nije NA npr.

Slicno pretpostavi da nije 1-1.

Ako npr. nije 1-1 onda postoje razliciti x,y za koje vazi

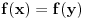
npr.

Probaj s ovim da petljas!

Sta je onda sa ?
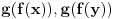
[ Sladjan2S @ 23.11.2009. 20:57 ] @
Ok, to je dokaz injekcije(1-1) što sam uradio na isti način, ali ostaje dokaz surjekcije, što ne kontam baš najbolje.

Ako imamo g i g' i kompoziciju g(g'(x))(x)=y.. Za g postoji bar jedno rješenje po g'(x) jer je već rečeno da je g surjekcija, dobijamo dalje g'(x)=z. I ona ima rješenje po x jer je rečeno da je surjekcija, što na kraju znači da je i g(g'(x)) surjekcija..

Da li je to dovoljno za dokaz ili postoji možda precizniji način kako to dokazati?
[ petarm @ 23.11.2009. 21:09 ] @
Dovoljno je! To je to.
[ Sladjan2S @ 23.11.2009. 21:27 ] @
Ok, hvala na pomoći.