[ Mlatko @ 24.11.2009. 00:10 ] @
|
[ petarm @ 24.11.2009. 10:36 ] @
@ keti
vec povrsinska gustina naelektrisanja u centru jednaka 0 i prema obodu raste proporcionalno kvadratu rastojanja od centra. Citat: Mlatko: Koncept bi trebao izgledati ovako: Posto je sigma proporcionalno kvadratu udaljenosti, to je 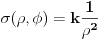 . . Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|