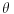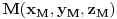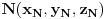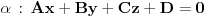[ pailhead @ 27.11.2009. 04:28 ] @
| Kao prvo, moram da kazem da sam arhitekta, a ne matematicar, i da se bavim kompjuterskom grafikom, a nazalost ne programiranjem. Problem je sto sam nedavno nabasao na program, u kome moze da se programira bez koriscenja jezika, samo povezivanjem razlicitih komponenti u grafickom okruzenju. Na raspolaganju je i dosta matematike, ali malo po malo pa negde zapnem. Dakle, Naprvio sam parametarsku piramidu, odnosno ortogonalnu matricu piramida. Nebitan je njihov broj, bitno je da svaka ima kvadratnu osnovu i da je ona konstante velicine. Visina h se menja, i na toj osi visine, na nekom h1 rastojanju od baze, nalazi se neka tacka. I h i h1 su promenljive, ali su iste za svaku piramidu. Kroz tu tacku, kroz svakuj piramidu, prolazi jedna ravan i sece je. Orijentacija ravni je odredjena vektorom, koji je za svaku piramidu zaseban, i preuzet iz jedne liste. Svaki taj vektor, moze imati komponente x i y od -1 do 1, ali komponentu z od 0 1 plus opet neka promenljiva vrednost x jer mi 0 ne odgovara, potrebno mi je da ta ravan ne gradi nikako ugao od 90 stepeni sa bazom. Dakle sa tim x koje dodam, odredjuem maksimalni ugao koju ravan moze da gradi sa bazom piramide. E sad, problem koji mi se javlja je, sto taj program, kada zadam veci broj piramida uzasno sporo radi, i moram po nekoliko minuta da cekam da mi generise resenje. Ono sto mi se moze desiti je da zaam vrednost x, tako da se u hiljadu piramida javi par gde ravan sece i bazu a ne samo strane kako mi treba. Meni je potrebno da nekako unapred predvidim, kolika ce biti najveca visina tog preseka u Z pravcu, odnosno tacnije rastojanje u Z pravcu od tacke kroz koju prolazi ravan, do najnize tacke preseka sa piramidom. Kada bi piramida bila beskonacna, mogao bih u tom rpogramu lako da generisem listu svih tacaka svih preseka, i da nadjem onu koja ima najnizu Z kordinatu, i to jednostavno oduzmem od Z kordinate one polazne tacke (visina h1). Medjutim, ne mogu da uacujem i to, jer bi to neverovatno opteretilo tu skriptu i pitanje je da li bi uopste program to izdrzao. Ako pokusam to da uradim na ovaj nacin na koji sad radim, opet necu znati, jer ce najniza tacka biti presek sa bazom, ako preteram sa onim uglom i nista mi nie znaci jer necu znati za koliko treba da povecam visinu ili ugao da ravan ne bi sekla bazu. Zanima me da li je moguce nekako uraditi neku funkciju sa vektorima iz te tacke, ili uglovima i na osnovu toga predviteti tu velicinu? Znam da bi najnizu tacku dala ravan cija je nagibnica pod 45 stepeni gledano u osnovi (lezi u zracnoj ravni u odnosu na bazu koja sadrzi dijagonalu) i koja bi imala najveci ugao u odnosu na bazu. Medjutim, ne znam sta se desava kada recimo imam neku ravan koja gradi veliki ugao (najveci ugao) sa bazom, ali je zato nagibnica (u osnovi gledano) blize uglu od 90 stepeni sa ivicom piramide, i kad imam neku drugu ravan, koja je pod manjim nagibom u odnosu na bazu, ali je ugao u osnovi mnogo blizi dijagonali. Trebalo bi nekako ta dva ugla, ili te vektore da objedinim, i tu da nadjem neku najvecu vrednost, koju bih kasnije iskoristio da dobijem tu visinu u odnosu na h piramide, i h1 te tacke. |