1. Nauči da pišeš formule u -u, daleko je lakše pratiti takav tekst a za ovo što ti hoćeš da pitaš ti ne trebaju neke spektakularne naredbe.

2. Princip je taj da treba da kažeš gde si zapeo, a ne da navedeš listu zadataka i očekuješ da ti ih neko reši. Kao što je navedeno u pravilniku, ovo nije servis za rešavanje zadataka. Dakle, kako si pokušao da rešavaš te zadatke i šta je problem?

Da li je problem ako formule ne pišem u -u?

Što se tiče zadataka potrebna mi je cela izrada, jer stvarno imam problema sa tim zadatcima...

Ne, naravno. Mada bi bilo poželjno, kao što sam i rekao.

Mnogo veći problem je ako se neko uopšte ni ne potrudi da reši zadatke pre nego što postavi pitanje. Moraš bar probati na neki način da uradiš zadatak/zadatke.

Obnovi teoriju, uradi neke lakše zadatke, pa ako ni onda ne ide, javi gde je zapelo. Odgovor „na početku“ nije dovoljno dobar, jer znači da nisi želeo ni da uložiš napor da razmisliš o problemu.

Ti zadatci su bili kontrolni. Dobio sam keca profesor mi nije naznacio greske rekao je da sam skontam, a posto ja nisam mogao da skontam potrazio sam pomoc od vas "forumasa".

Pa, napiši kako si ti radio, pa da vidimo gde su greške. Ovako ispada da dolaziš na forum jer te mrzi da pogledaš u knjigu i svesku.

Nemaš ništa od toga ako ti neko uradi zadatke, gledaćeš u njih, mislićeš da razumiješ i tome sl. i vec idući put ćeš dobiti ponovo keca. Obično to tako ide...

Zašto ne pokušaš da uradiš sam kod kuce zadatke pa makar bili 100% netačni, odneseš profesoru da pogleda i uputi te kako dalje da radiš? I tako sve iznova i iznova dok nešto ne naučiš...

Daću ti ovdje uputstva a ti se potrudi da ih sam uradiš:

1. Rješenja su (realna i) jednaka ako i samo ako je je D=0; diskriminanta D određuje prirodu rješenja kvadratne jednačine; odredi koeficijente a, b i c, uvrsti u formulu za D i izračunaj za koju vrijednost parametra m je zadovoljena gornja jednakost;

2. Svedi kvadratnu jednačinu na normalni oblik, odredi koeficijente p i q, zatim ih uvrsti u Vijetove formule; zadani izraz je zbir dva razlomka, kada ih saberes zamijenićeš izraze u imeniocu i brojiocu vrijednostima dobijenim u Vijetovim formulama;

3. Rastavi imenioce algebarskih razlomaka na činioce, postavi odgovarajuće uslove (u imeniocima razlomaka ne smiju biti nule), odredi NZS kojim ćeš pomnožiti cijelu jednačinu da se riješiš razlomaka, prebaci sve na lijevu stranu odredi parametre a, b i c i primjeni formulu za rješavanje kvadratne jednačine;

4. vidi 3.

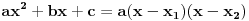
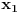
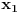
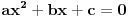
5. Koristeći formulu gdje su i rješenja kvadratne jednačine (ili na neki drugi način, ponovi rastavljanje polinoma na činioce) rastavi imenioc i brojioc razlomka na činioce zatim pokrati iste;

6. Primjeni Vijetove formule da odrediš p i q, zatim ih uvrsti u normalni oblik kvadratne jednačine; podrazumijeva se da znaš sabirati i množiti kompleksne brojeve.

^Sini82, hvala ti pomoglo mi je dosta.

Sto se tice petog zadatka kod formule , dobijem da su mi i , iz formule dobijem da su mi i .
Zatim to uvrstim u formulu i dobijem , da li je to tacno? Da li bi mogao da mi to preformulises i da izmnozis, posto mi to bas ne ide?

Kod sestog zadatka takodje koristim formulu i dodjem do ovog dela i zatim to treba da se skrati sa 7 i da li to onda ispadne ovaj izraz ako jeste onda ga uvrtsim u formulu , e tu sam stao uvrstim i ne mogu dalje... Da li mozes to da mi dovrsis, da vidim kako to izgleda?

6*X^2 + X - 12 = 0

D = b^2 - 4*a*c = (1)^2 - 4*6*(-12) = 1 + 288 = 289.

Koren(289) = 17.

Tako da jednačina 6*X^2 + X - 12 = 0 ima realna rešenja X1 = 4/3 i X2 = -3/2.

Pa je 6*X^2 + X - 12 = 6*(X-4/3)*(X+3/2) = (3*X-4)*(2*X + 3).

Aj reši ispravno bar ovu drugu: 12*X^2 - 31*X + 20 = 0 jer i ona ima realna rešenja.
Ne kapiram kako si nju mogao da uprskaš jer su i a i c pozitivni.
Kod prve sam imao razumevanja da si se zezno zbog negativnog a koeficijenta.

Kec je velika ocena za ovakve "bisere".

to se ne resava preko , nego preko naravno to mi je profesor rekao...

Ja trazim pomoc, a dobijem uvredu, strasno...

Ispravke i uputstva (zadaci 5. i 6.):

5. ; dati kvadratni trinom rastavi na činioce analogno kao i prethodni (kako ti je uradio miki069);

6. ; nisi dobro izračunao q (pomnoži data dva kompleksna broja ili primjeni formulu za zbir kvadrata)
; p si dobro izračunao ;

Jednačinu koju si dobio trebaš da pomnožiš sa 49 jer je on zajednički za 7 i 49 a ne sa 7; onim množenjem nisi ništa postigao, nisi se riješio razlomka;

miki069 je takođe u pravu, možeš prvo da izračunaš D pa da primjeniš formulu

@Sini82, hvala ti.

Ja sam ti napisao samo izraz pod korenom b^2 - 4*a*c koji određuje da li jednačina ima ili nema realna rešenja.
Taj izraz se naziva diskriminanta, jer diskriminiše, i obeležava sa D.

Taj izraz nisi izračunao ispravno ni u jednom zadatku i ja sam ti skrenuo pažnju gde si grešio u izrazu iz brojioca.
Isti sam ti kompletno uradio i posavetovao te da sam uradiš izraz u imeniocu.
Preskočio sam samo korak kada se broj 6 rastavlja na 3*2 i sa 3 množi prva zagrada, a sa 2 druga zagrada.
Sve ti je već Sini82 servirao i napisao, ali da uradiš samostalno ostale zadatke.
Ne kapiram gde sam te ja uvredio i šta je u mom rešenju bilo "strašno"...???

Ako si uradio samostalno zadatke i nešta naučio onda je cilj postignut i nije ni bitno što je to bilo "strašno".

Pozdrav