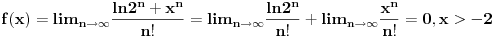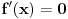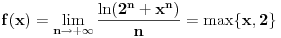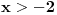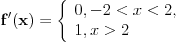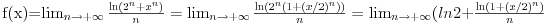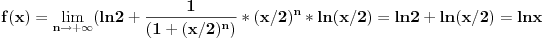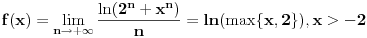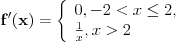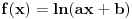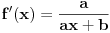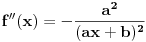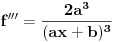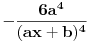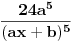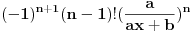izvod nevjerovatne funkcije

[ mathelp @ 06.12.2009. 02:24 ] @

pozdrav svima! trebam rijesiti jednu funkciju, ali u njoj postoje x i n, pa me to buni. zadatak glasi:
odrediti prvi izvod funkcije:
f(x)=lim( (ln((2^n)+(x^n)))/n ) , (x>-2) Ispod limesa n -> oo.
Oprostite sto je necitko napisano, ova dva sabirka su u brojniku, n je u nazivniku, a limes ispred razlomka.

_{[Ovu poruku je menjao mathelp dana 06.12.2009. u 03:50 GMT+1]}

_{[Ovu poruku je menjao mathelp dana 06.12.2009. u 03:54 GMT+1]}

[ petarm @ 06.12.2009. 03:19 ] @

[ Nedeljko @ 06.12.2009. 08:55 ] @

[ h4su @ 06.12.2009. 12:06 ] @

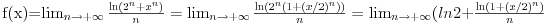
za x<2 f(x)=ln2
za x>2

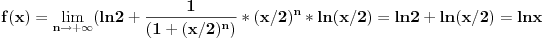
uz pomoc lopitala

uglavnom, ako nije mozel detaljnije nedeljko

[ Sini82 @ 06.12.2009. 12:37 ] @

Ja sam radio na drugi nacin, takodje sam isto dobio, ispravka kod Nedeljka:

.

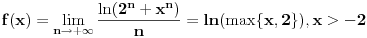
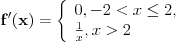
_{[Ovu poruku je menjao Sini82 dana 06.12.2009. u 13:50 GMT+1]}

[ mathelp @ 06.12.2009. 15:56 ] @

Jel moze dodatno objasnjenje, molim vas? Kako se dobije ovo max, i sta ono predstavlja, te kako na kraju zakljucujem sta je prvi izvod?!

[ Sini82 @ 06.12.2009. 17:26 ] @

max{x,2} je x ako je x>2 a 2 ako je 2>=x.

Dakle, f(x)=lnx za svako x>2 a f(x)=ln2 za svako x<=2 tj. -2<x<=2 jer vrijedi x>-2.

Nakon toga trazis izvod funkcije na datim intervalima (poluintervalima).

[ mathelp @ 06.12.2009. 18:11 ] @

Da, da, sad mi je jasno za izvod. Samo jos mi nije jasno ovo za max. Kako se to dobilo iz pocetne funkcije, i sta predstavlja (je li to neka maksimalna vrijednost funkcije ili...)? Tj. zasto je vrijednost funkcije lnx na intervalu x>2, a ln2 na -2<x<2?

[ devetkamp @ 12.01.2013. 10:31 ] @

Jel moze neko da mi pomogne oko nalazenja n-tog izvoda funkcije

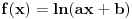
?.... Hvala :D

[ Fraktal @ 12.01.2013. 12:28 ] @

Prvi izvod je:

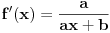
Drugi:

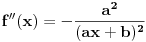
Treći:

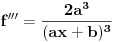
Četvrti:

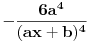
Peti:

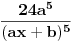
Lako je opaziti pravilnost u samom postupku diferenciranja, tj. da je n-ti izvod jednak:

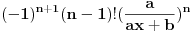
[ devetkamp @ 12.01.2013. 13:14 ] @

Hvala. A da li moze zadatak da se uradi i na neki drugi nacin? Npr Lajbnicova formula...