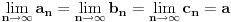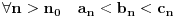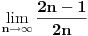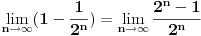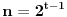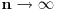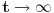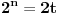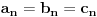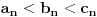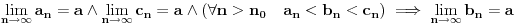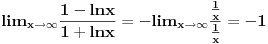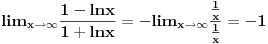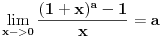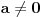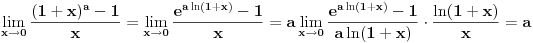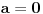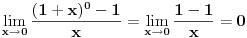limesi-zadatak i teorema

[ Adnaaa @ 08.12.2009. 23:38 ] @

Pozdrav:-)

lim(kada n tezi + beskonacno) od (2n-1)/2n je ekvivalentno lim(n tezi + beskonacno) od (1- 1/2^n)

ovaj drugi lim je 1 - 1/2 na n,n je eksponent na 2.

Treba mi pomoc pri rjesavanju ovog zadatka jer jos nisam radila slicne zadatke,dokazivanje ekvivalencije kod limesa.
Unaprijed hvala.

Takodjer imam zadatak da dokazem teoremu:

lim an = a , lim bn = a , lim cn = a (n je u indeksu,ispod svakog limesa je n tezi +beskonacno)

dokazati da vrijedi an<bn<cn za svako n iz skupa prirodnih brojeva.

Pokusala sam sa | an -a | < od epsilon , (a-epsilon,a+epsilon) medjutim,stalno se "vrtim u krug".

_{[Ovu poruku je menjao Adnaaa dana 09.12.2009. u 00:50 GMT+1]}

[ Cabo @ 09.12.2009. 15:31 ] @

Primeni teoriju: teoreme koje ste radili na časovima, raspiši cele izraze za limes funkcije, itd. Kod nekih teorijskih zadataka se traže i dodatne „cake“: da pomnožiš ili podeliš izraz nekim koeficijentom, dodaš i oduzmeš neku vrednost pa dobiješ kraći izraz...

To je, uopšteno, princip po kome se dokazuju teorijske stvari iz Matematike. Slično se ispituje i da li je neka funkcija diferencijabilna, neprekidna...

P.S.: Iz

uopšte ne sledi da je

. Mora da je tu bio još koji uslov...

[ Sini82 @ 09.12.2009. 16:21 ] @

Limesi

su ekvivalentni jer se prvi limes svodi na drugi limes smjenom

(kada

tada i

) a drugi na prvi smjenom

(kada

tada i

).

Za drugi zadatak mozemo naci bar jedan kontra primjer. Posmatrajmo nizove za koje važi

za svako

; za koje očigledno važe uslovi zadatka a ne važi

ni za jedno

.

_{[Ovu poruku je menjao Sini82 dana 09.12.2009. u 17:34 GMT+1]}

[ Adnaaa @ 09.12.2009. 21:45 ] @

Hvala vam puno na odgovoru,puno mi je pomoglo. :-)
A to se tice teoreme, ako je liman=a i limcn=a i imamo an<bn<cn,onda slijedi da je i limbn=a.
Znam da je prof. govorio da ne mora biti zadano limbn=a,nego da slijedi iz ovoga.

[ Cabo @ 10.12.2009. 17:56 ] @

Citat:

Adnaaa: A to se tice teoreme, ako je liman=a i limcn=a i imamo an<bn<cn,onda slijedi da je i limbn=a.
Znam da je prof. govorio da ne mora biti zadano limbn=a,nego da slijedi iz ovoga.

Ovako već može.

se zove „teorema o dva policajca“.

Ali, uopšte ne važi ono što si ti napisala u prvoj poruci, što je Sini82 demonstrirao kontraprimerom.

_{[Ovu poruku je menjao Cabo dana 10.12.2009. u 19:52 GMT+1]}

[ saxhax @ 25.03.2010. 21:24 ] @

.....1-lnx
lim ——— =?
.....1+lnx
Dali neko zna:::?
Tačke su nista, aisprekidane crtice su razlomacka crta

[ zzzz @ 25.03.2010. 23:31 ] @

Čemu teži x?U beskonačnost ili ..

[ saxhax @ 26.03.2010. 09:16 ] @

Sorrrrrrry
Trazi se H. asimptota...
tada x→beskonacnost

[ petarm @ 26.03.2010. 11:52 ] @

Lopitali