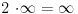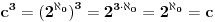A šta smatraš pod tačkom?
Polaziš od pretpostavke da ona ima fizičke dimenzije? (širinu, dužinu, obim, površinu,...)
I kako interperetiraš tačku? kao kružić, kvadratić, pravougaonik, trouglić,...?

Vezano za temu i skup prirodnih brojeva ima istu moć(isti broj elemenata) kao i skup parnih prirodnih brojeva.

Dolazio si ti i ranije do mnogih čudnih zakjučaka.

Svaki beskonačan skup se može bijektivno preslikati u svoj pravi deo. Nije ništa čudno što se duž može bijektivno preslikati na svoj pravi deo, jer je duž beskonačan skup tačaka. No, to znači da duž ima najmanje toliko elemenata koliko i ona sama.

Skupovi se po broju elemenata (kardinalnom broju) porede na sledeću način:

Ako postoji bijekcija izmežu skupova, kaže se da imaju isti kardinalni broj.
Ako se skup A može 1-1 preslikati u skup B, kaže se da skup A ima manji ili jednak kardinalni broj od skupa B.
Ako se skup A može 1-1 preslikati u skup B, a ne postoji bijekcija između njih, kaže se da skup A ima manji kardinalni broj od skupa B.

Možeš ti jednoj duži dodati drugu duž, ali time nećeš povećati kardinalni broj.

Duž je beskonačan skup tačaka. Skup je beskonačan ako ima isti broj elemenata kao neki njegov pravi podskup, što nikako ne može da bude osobina konačnih skupova. To ne znači da duž sadržana u duži sadrži u sebi manje tačaka od duži u kojoj je sadržana. One sadrže u sebi isti broj tačaka, što se pokazuje tako da se među njima uspostavi bijekcija (obostrano jednoznačno preslikavanje).

Beskonačan skup ima prebrojivo mnogo ili neprebrojivo mnogo elemenata zavisno od toga da li je uspostavljena bijekcija sa skupom N ili sa skupom R. Svaka duž ako su joj početna i krajna tačka različite sadrži neprebrojivo mnogo tačaka.

Bijekcijom se prebrojavaju i konačni i beskonačni skupovi.

Primjer 1.

Skup malih slova abecede ima 30 elemenata jer vrijedi {a,b,c,...,ž}~{1,2,3,...30} (bijekcija sa konačnim podskupom skupa N).

Primjer 2.

Skup cijelih brojeva ima prebrojivo mnogo elemenata jer vrijedi Z~N (bijekcija sa skupom N).

Primjer 3.

Skup tačaka na intervalu (0,1) ima neprebrojivo mnogo elemenata jer vrijedi (0,1)~R (bijekcija sa skupom R).


Ako te zanima više potraži na internetu.

Pa niste mi baš pomogli - ja sam poslao i crtež i pitao sam gde je konkretno
greška a vi mi odgovarate tako da mi se čini kao da crtež niste ni pogledali

Postoje beskonačni skupovi koji se ne mogu bijektivno preslikati ni u skup N, ni u skup R.

Pogledali smo crtež. Nije crtež pogrešan, nego tvoje tumačenje crteža. Ili nisi pažljivo pročitao naše odgovore?

U pravu si Nedeljko. Pokušao sam što više da mu pojednostavim. Tačnija definicija bi bila da je skup neprebrojiv ako nije prebrojiv.

Npr. P(R) ?

Da, P(R) je jedan od primera.



To što skup ima isto elemenata kao njegov pravi podskup ne znači da ima više elemenata od sebe samog.

Ha ha, samo vas gledam.

Naš stari drugar Galet se ponovo javlja, sa njegovim teorijama o pogrešnosti Analize i čitave matematike.

Kako ne shvatate, ne vredi mu objašnjavati, čovek neće da sluša da mu je način razmišljanja pogrešan jer ne sledi principe matematičke logike. Ne hranite trola.

Hvala na "lepim" rečima - nažalost ja nemam pravo da uzvratim istom merom jer će tema
po običaju biti zaključana
Ali ipak se usuđujem da pokažem šta ja mislim o tome u prilogu koji se odnosi na bijekciju
dužina.

Dane, probaj da tačke iz kvadrata preslikaš na duž. Videćeš da ih u kvadratu ima više nego na duži. Da ne govorim o preslikavanju tačaka iz kocke.

Otprilike, dolazimo do pitanja da li je ili ne, tj. da li je duplo vece od ili ne
Da li sam pravilno shvatio dilemu tj. tvrdnju Dane?

Ne znam kako da to uradim, ali mi se čini da na duž možeš da staviš koliko god hoćeš
tačaka jer tačka ionako nije ništa. Ovim ne negiram tačku kao geometrijski objekat
niti njeno začenje u definisanju nekog mesta na duži, ravni ili u prostoru. Možda bi
bolji naziv za tačku bio "mesto", ali to nije bitno

A skontao sam tek pošto sam već poslao poruku - verovatno se radi o tome da se
određene duži kvadrata preslikavaju u samo jednu tačku na duži na koju
preslikavamo

_{[Ovu poruku je menjao galet@world dana 12.12.2009. u 09:07 GMT+1]}

Sasvim!
U konkretnom jednostavnom slučaju radi se o tome da je odnos dužina crvenih i
plavih intervala jednak 2. Upravo taj odnos koji je nezavisan od broja intervala
ostaje nepromenjen i ako je broj intervala beskonačan. Očuvanje odnosa nam
daje mogućnost da nešto saznamo i o beskonačnostima. Očuvanje odnosa je
izuzetan princip koji jednako važi (bar mi se tako čini) za konačne, beskonačno
velike i beskonačno male veličine.
Deljenjem neke duži na beskonačno mnogo jednakih (ili različitih - svejedno)
intervala ne ukida se dimenzija dužine tih intervala jer je obrnutim postupkom
moguće da opet dobijemo tu duž - hoću da kažem na taj način ne možemo
dobiti tačke jer one nemaju dimenziju dužine.

Postoji bijekcija du\i na ceo prostor. .

Ako je tako, Dane - ti si u pravu!

Smem li da pitam u vezi čega je u pravu?

Naravno da smeš. Zašto ne bi smeo?

Npr. Neka duž leži unutar kvadrata (kraća je od dijagonale!). Očigledno je da možeš napraviti bijekciju svih tačaka kvadrata koje istovremeno pripadaju i duži na tačke koje pripadaju samoj duži. Šta je sa ostatkom tačaka kvadrata?

Nisam baš siguran da sam te razumeo, ali moj odgovor bi bio da se na duž unutar
kvadrata (koja nije dijagonala) može preslikati deo tačaka kvadrata, ali ne sve

I gde je odgovor?

Pa valjda prvo ide pitanje?

:-)

U međuvremenu nepar natuknica za razmišljanje:

- dužina duži ne zavisi od "količine" tačaka na njoj (valjda?).
- skup sa beskonačno mnogo elemenata ima više elemenata nego bilo koji njegov podskup (koji takođe može imati beskonačno elemenata) - ovako i Dane razmišlja o skupu tačaka neke duži ("duž ima više tačaka od sebe same" )
- kako upoređivati beskonačne stvari, da li "jedno beskonačno" može biti veće od "drugog beskonačnog" i koliko?

Da li možemo prvu sliku da gledamo ovako:

- SVE tačke duži A'B' su preslikane na tačke duži AB.
- pošto su ostale nepreslikane tačke sa duži CA' i B'D, očigledno je da na AB postoje tačke na koje ne postoji nikakvo preslikavanje
- odavde sledi da pomenuto preslikavanje (A'B' na AB) nije biunivoko.

<sub>[Ovu poruku je menjao Fitopatolog dana 13.12.2009. u 12:39 GMT+1]

[Ovu poruku je menjao Fitopatolog dana 13.12.2009. u 16:39 GMT+1]</sub>

Kako onda objašnjavaš činjenicu da bijekcijom proizvoljnoj tački jedne duži
možemo da pridružimo tačku druge duži (naravno i obratno)?



Tačno. Dužina duži ne zavisi od broja tačaka, broj tačaka na duži je invarijanta,
sve duži imaju isti broj tačaka - neprebrojivo mnogo (c).



Logika koja važi kod konačnih skupova ne važi kod beskonačnih skupova. Kao što sam
već napisao i jedni i drugi se prebrojavaju bijekcijom. Ta osobina da skup ima onoliko
elemenata koliko i njegov pravi podskup se i uzima za definiciju beskonačnosti. Uzmimo
za primjer prirodne i parne brojeve:

1 <-> 2*1
2 <-> 2*2
1 <-> 2*1
.
.
.
n <-> 2*n
.
.
.


Skup parnih brojeva je pravi podskup skupa prirodnih brojeva. Kao što vidiš ima ih isto,
iako bi prvo pomislio da prirodnih brojeva ima duplo više nego parnih.



Mogu se uspoređivati beskonačne veličine i to preko kardinalnih brojeva o čemu je u ovoj
temi Nedeljko već pisao.

Tačka? Šta li je tačka?

Šta bi značilo da su sve beskonačne veličine jednake?

Uzima se - ali kako se dokazuje?

(Zašto su ti prvi i teći red jednaki?)
U bilo kom konačnom parnom pirodnom broju - broj parnih (ili neparnih) brojeva je dvostruko
manji od od tog broja. Ovaj odnos ne zavisi od veličine tog broja
Taj odnos se ne menja - a i zašto bi -bez obzira na bilo koji (ili koliki) broj parnih brojeva
uključujući i beskonačnost
Tvrdnja da parnih brojeva ima isto toliko koliko i prirodnih je u suprotnosti sa (mojim?)
principom očuvanja odnosa
Odnos broja nekih brojeva prema broju prirodnih brojeva ne zavisi od načina pridruživanja tih
brojeva prirodnim brojevima niti je to dokaz jednakosti broja elemenata podskupa sa brojem
elemenata skupa. Jedini univerzalni dokaz je pomoću
očuvanja odnosa ili zakonitošću promene tih odnosa koji jednako važe za sve brojeve

Na isti način

Nauči šta znači reč definicija.

Ovo je forum Matematika, i u njemu se raspravlja na osnovu matematičkih principa, a ne „tvojih“ principa. Kako, dakle, ovo nema veze s matematikom, temu zatvaram.