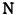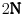Čoveče, shvati da je pojam beskonačnosti poseban pojam u matematici. To brucoši na Matematičkom ili savladaju iz Analize 1, ili napuste studije matematike.

Beskonačnost nije broj i beskonačni skupovi se ne ponašaju isto kao skupovi sa konačnim brojem elemenata (namerno koristim baš te konstrukcije, „beskonačni skupovi“ umesto „skupovi sa beskonačnim brojem elemenata“ i „skupovi sa konačnim brojem elemenata“).

Odnos između konačnih i beskonačnih veličina predstavlja suštinu Računa (Calculus), grane matematike čiji je Analiza (1 i 2) samo jedan deo.

Pojam beskonačnosti je strogo definisan aparatom matematičke logike. Ponavljam, to nije realni broj.

Ti se možeš nad tim iščuđavati, ali to je tvoja privatna stvar i predstavlja zatrpavanje foruma besmislenim porukama.

Kako ti nije jasno da

1. On ne zna šta je skup.
2. Ne želi ni da sasluša standardno zasnivanje matematike.

Pa ovde je rekao



:-S

Problem u tvom shvatanju je sto si postavio ovaj uslov koji si naglasio, tj da se mogu koristiti SAMO kartoncici s nacrtanim prirodnim brojevima.
Naime, da bi uopste pricao o bijekciji, odnosno da bi usporedjivao broj elemenata, trebas imati DVA skupa, zar ne? I vec zbog toga uslovu koji si naveo nema mjesta u ovoj prici.
A ti to nisi napravio, nego si samo na kartoncicima iscrtao elemente JEDNOG skupa i pokusao isparivati njegove elemente.
Nadam se da shvatas u cemu je problem?

Skup prirodnih brojeva i skup parnih brojeva su DVA skupa, koja u nasem problemu promatramo potpuno neovisno jedan o drugome, i grijesis ako mislis da se npr dvojka ne moze pojaviti u oba.

Dakle ono sto si trebao napraviti je da napravis DVA skupa kartoncica: jedan na kojima su nacrtani prirodni brojevi, a drugi na kojima su nacrtani parni brojevi:
skup A: 1, 2, 3, 4, 5, 6, 7, ...
skup B: 2, 4, 6, 8, 10, 12, 14, ...

I sad samo napravis parove na nacin da uzmes prvi element iz skupa A i pridruzis mu prvi element iz skupa B, pa onda uzmes drugi element iz A i pridruzis mu drugi element iz B, itd.
Na taj nacin dobijas ono sto si trazio, tj svakom prirodnom broju si pridruzio (razlicit) parni broj.

Mlatko, problem je što bijekcija između skupova 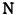i 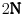ne može da se predstavi u prirodi. Skup 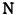ne postoji u prirodi. Predmet proučavanja matematike su apstraktni objekti.

I to je problem sa fizičarima i ostalim tzv. „običnim svetom“: oni bi hteli sve da pokažu „primerima iz prirode“ (postoji već tema). Matematika se ne može objasniti „primerima iz prirode“. Samo se neki od prirodnih procesa mogu idealizovati matematičkim modelima.

Ne vidim nigde u ovoj temi razlog da prozivas fizicare! U temi o kojoj je bilo rasprave je pricano o tome da ne treba celu matematiku predavati kao niz teorema, dokaza, definicija... Ja sam rekao da matematiku ne mozes na isti nacin predavati matematicarima, fizicarima i inzenjerima. Ako za nesto u matematici postoji primer iz prirode (sto je veoma cesto slucaj u matematickoj analizi) korisno je to naglasiti zbog shvatanja same problematike!

Petre, ne treba da se žestiš, Savo je izuzeo vas fizičare od "običnog sveta" - kako sam ja razumeo, radi se o dva disjunktna skupa...

Uzgred, zar nismo VEĆ apsolvirali u nekoj ranijoj temi da je i SAMA matematika deo prirode?

Uh - koliko odgovora! Zahvaljujem.
Ja sam pretpostavio da i vi mislite na postojanje samo jednog skupa A prirodnih brojeva,
naravno, sa njegovim podskupovima

Moje pitanje je sasvim jednostavno:
da li se oni kartončići mogu složiti u tražene parove koristeći članove samo tog skupa
ili ne mogu?

Ako mogu onda vas molim da pokažete kako.

1 <---> 2
2 <---> 4
3 <---> 6
...
...
itd...

Dane, napiši POSLEDNJI član u nizu, pa da PREBROJIMO kojih je više...


p.s. pogledaj takođe i http://tesla.rcub.bg.ac.yu/~spiral/Math/Kardinalni%20brojevi.htm


_{[Ovu poruku je menjao Fitopatolog dana 17.12.2009. u 22:05 GMT+1]}

Naravno, NEMA poslednjeg člana jer brojeva 1,2,3,4.... ima beskonačno mnogo. Ali, uz svaki taj broj 1,2,3,4,... pridružen je po jedan parni: 2,4,6,8,... Kako? Pa i parnih ima beskonačno, ne može da ih nestane... Ludilo! I da pridružujemo umesto parnih brojeve 1000000,2000000,3000000,4000000,... opet je ista situacija! I njih ima koliko i celih, koliko i parnih brojeva - PREBROJIVO mnogo.

Ali, do konačnog broj M ima samo M/2 parnih! Baš nas briga za to, od M pa do beskonačno ima beskonačno i parnih i celih brojeva! Šta je M ili M/2 prema beskonačnom broju?

Napravili ste konstrukciju sa kartonićima, djeca bi to mnogo bolje uradila.

Dječaci bi obojali kartoniće sa prirodnim brojevima jednom bojom, djevojčice kartoniće sa parnim brojevima drugom bojom, sparivali bi jedne sa drugima i tako u nedogled bez ikakvih problema.

Zbunjuje vas to što je skup parnih podskup skupa prirodnih brojeva? Što se brojevi na kartonićima jedne boje duplo manji (veći) od brojeva na kartonićima druge boje?

Djeca bi vidjela ono što vi ne vidite, da kartonića ima isto. U igri bi nalijepila sličice autića na kartoniće jedne boje i sličice barbika na kartoniće druge boje, da vas brojevi ne zbunjuju, za malu dječicu to su nerazumljive šare na kartonu.

Kartonići bi i dalje ostali upareni, niko ne bi gledao ni koji je autić brži, ni koja je barbika ljepša. Svaka barbika bi stajala kraj njoj dodjeljenog autića i svaki autić bi imao kraj sebe njemu dodjeljenu barbiku.

Ali Dušane odakle ti dve dvojke? Nadam se da ne teoretišem na "moj" način ako
kažem da skup A prirodnih brojeva sadrži svaki prirodni broj samo jedamput.
Već u sledećem redu bila bi ti potrebna još jedna četvorka i t. d. zar ne?



Ako bi dečaci obojili kartončiće sa prirodnim brojevima jednom bojom, šta bi ostalo
devojčicama da farbaju?

Nema greške! Imamo "dve korpe": U prvoj su brojevi 1,2,3,4,... a u drugoj 2,4,8,.... Jedna dvojka je iz jedne korpe a druga iz druge. Ima li neuparenih brojeva iz prve korpe? Nema! Ima li neuparenih brojeva iz druge? Nema! Ima li dvaput (ili više puta) uparenih brojeva iz bilokoje korpe? Nema! Ludilo opet!

Bijekcija f:A->B je pridruživanje svakom elementu skupa A po tačno jednog elementa skupa B tako da je svaki element skupa B pridružen tačno jednom elementu skupa A. To što isti objekat pripada različitim skupovima nije nikakav problem.

Model u školi bio bi sledeći: Svaki kartončić se podeli na dva dela. Jedan se obeleži sa "original", a drugi sa "slika". Najpre dečaci upišu u "original" delove sve prirodne brojeve - svaki prirodan broj na tačno jedan kartončić, tako da potroše sve kartončiće. Zatim devojčice upišu parne brojeve u "slika" delove kartončića - svaki na tačno jedna kartončić, ali tako da na kraju svi kartončići ostanu popunjeni. Dakle, kartončići nisu bukvalno prirodni brojevi, već samo formulari za popunjavanje.

Ja sam upotrebio konjunkciju: 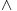. „Običan svet“ „ljudi koji nisu studenti matematike niti diplomirani matematičari“.


Matematika nije deo prirode u nebukvalnom (čitaj: pametnom) smislu. Što će reći: to što po materijalistima misao kao impuls u mozgu postoji u fizičkom svetu ne znači da u fizičkom svetu postoje zmajevi i hobiti.

DODATAK: Inače bi postojao i ovaj baja:



Kad Orson nešto zamisli, to se stvori u prirodi. :-S

_{[Ovu poruku je menjao Cabo dana 18.12.2009. u 15:10 GMT+1]}

Matematika je formalna nauka, koja je primenljiva u mnogim naukama, pre svega prirodnim, ali i drugim (lingvistici npr.). Daleko od toga da je deo prirode.

@ Cabo

Dobro za tebe! Ne moras ni da zavrsis matematiku! Vec si neobican! :)

Nastojim da divergiram (da mi ostatak ne bi težio nuli).

Hm, možda i ovo što kažete može da bude konzistentno: Matematičari su neobični ljudi a matematika je neprirodna nauka?

Lako je tebi kad imaš dve korpe – tako bih i ja znao da složim parove –
ali ja to ne mogu da uradim sa brojevima samo iz jedne korpe koja sadrži
skup A prirodnih brojeva – fali mi parnih – mogu samo da složim parove
koji sadrže jedan parni i jedan neparni broj.

SUPER! Ovo znači da si razumeo i prihvatio objašnjenje!



... međutim - ovde već počinje kontriranje... Pa dobro, smisli nešto da valja pa ćemo to nazvati KANTOR-DANETOVOM tezom o beskonačnim skupovima...

Zašto bi to devojčice radile AKO u skupu prirodnih brojeva napisanih na
kartončićima imaju već gotove takve kartončiće sa već napisanim parnim
brojevima?
Ako u skupu A prirodnih brojeva ima jednako prirodnih i parnih brojeva
onda ne treba ništa drugo raditi osim slaganja parova.
Ako u skupu A prirodnih brojeva ima jednako prirodnih i parnih brojeva
sve je već urađeno osim uparivanja – a može li se to uraditi na direktan
način korišćenjem isključivo elemenata skupa A (bez raznoraznih pomoćnih
radnji)?

Savo sokole, samo nas GLEDAJ!

@galet@world

Jel moze jedna zagonetka?
Na konferenciju za stampu povodom neplasiranja reprezentacije na SP doslo je deset novinara. Nitko osim njih nije prisustvovao konferenciji.
Medju novinarima se povela zestoka rasprava oko toga treba li selektor ostati i dalje na celu reprezentacije.
Milojko je bio kritican prema selektoru i zahtijevao je da ovaj odmah odstupi.
Vladan mu se usprotivio i hvalio selektora na sva zvona.
Marko, Aleksandar, Dragica i Jelena su bili na Milojkovoj strani. Suzana, Jovana, Milivoj i Boris su zastupali Vladanovo misljenje.
Koliko je zena bilo na konferenciji?

<sub>[Ovu poruku je menjao Mlatko dana 18.12.2009. u 19:40 GMT+1]

[Ovu poruku je menjao Mlatko dana 18.12.2009. u 19:42 GMT+1]</sub>

Zato što je na svakom kartončiću kao formularu po jedna polovina ostala nepopunjena.

Kada pišeš knjigu, ti možeš istu reč da upotrebiš više puta. U čemu je problem. Različiti artikli mogu imati istu cenu itd.

A ne! Taman posla. A i obećao sam da ću samo da pitam. Kad bih rekao
šta sam ja smislio odmah bi se umešao moderator sa svojim rešenjem.

Zato sto se ovde radi o dva skupa, a ne jednom.



Ne moze.


Ti ovde nemas problema sa bijekcijom.

Ako je tako onda nema problema. Meni se učinilo da je skup prirodnih brojeva nešto
drukčiji od knjige i da u njemu nema ponavljanja elemenata skupa.

Ne treba više raspravljati o bijekciji - s njom smo dokazali(?) da u skupu prirodnih brojeva
ima isto toliko parnih koliko i prirodnih i tu je kraj.
Da li možeš konkretno i da pokažeš to što je dokazano?

Pa, naravno da u skupu prirodnih brojeva, kao i u svakom drugom skupu nema ponavljanja, ali to nema veze sa ovom temom.

Svakom artiklu u radnji je pridružena cena, koja predstavlja neki ceo nenegativan broj nekih novčanih jedinica. To što jedan artikal košta n dinara ne znači da neki drugi ne može imati istu cenu od n dinara. Na taj način je svakom artiklu pridružen neki ceo broj. On nije potrošen time što je upotrebljen za nešto - i drugi imaju pravo d aga koriste.

Možeš i skup preslikati u sebe. Recimo, na zabavu je došlo 5 bračnih parova i osim njih niko više. Njih desetoro obrazuju skup A. Svakom članu tog skupa pridružiš njegovog bračnog druga/drugaricu. Dakle, skup A si preslikao u skup A. Može i to. takođe, svaki skup možeš preslikati u sebe tako što svakom elementu pridružuješ isti taj element itd.

Zašto misliš da se radi o dva skupa?
Meni izgleda da se ne radi o dva skupa nego o jednom, a "dokaz" o svojstvima tog jednog
skupa je urađen pomoću dva skupa

Postojanje bijekcije je definicija posedovanja istog broja elemenata. Obrati pažnju na reč "definicija". Ovde smo u suštini pokazali da postoji bijekcija skupa prirodnih brojeva u skup parnih prirodnih brojeva, a to se kraće izražava rečima "imaju isti broj elemenata".

Kako da ti konkretno pokaže? U prirodi ne postoji beskonačnost.

Šta bi tek onda bilo da može konkretno da ti pokaže? Recimo da ti donese tvoju omiljenu knjigu od prebrojivo mnogo listova, iskine svaki drugi list, vrati ti je raskupusanu i kaže ti da knjiga ima i dalje isti broj listova koliko ih je imala prije kidanja beskonačno mnogo njih? Mislim da bi te sludio.

Baš zato što je beskonačnost nešto što ne postoji u realnosti, nego samo kao pojam u ljudskim glavama, dolazi do problema kada taj pojam sebi pokušaš da predstaviš i objasniš preko objekata iz tebi poznatog realnog svijeta.

Radi se o dva skupa:

1. Skup prirodnih brojeva N={1,2,3,...} i
2. Skup parnih brojeva 2N={2,4,6,...}.

Ne dokazuju se svojstva jednog skupa, nego jednakost broja elemenata ova dva skupa. Ti sam izvlačiš zaključke o svojstvima jednog od ta dva skupa, kao posljedicu jednakosti broja njihovih elemenata, koju nisi prethodno ni dokazao jer te ti unapred doneseni zaključci ograničavaju.

Zanimljiva rasprava.
Odmah na pocetku moram da naglasim da nisam upoznat sa svim teoremama i zakonima u matematici ali nemojte odmah da otpisete moj odgovor jer vam moze zazvucati interesantno.
Naime, poceo bih prvo od potrebe koriscenja brojeva (merenje nekih velicina, prebrojavanje nekih fizickih elemenata...). Morate se sloziti da brojeva nebi ni bilo da nije bilo ovih "prirodnih" potreba. Ove potrebe su prvo dovele spoznaje prirodnih brojeva, pa onda smo hteli da napisemo sta ce se desiti ako nemamo nikakvih elemenata ili neka duzina ne postoji, pa smo uveli i broj 0. Kasnije je bilo potrebno i zapisati koliko nam fali nekih elemenata ili koliko je neka fizicka velicina manja od druge pa smo uveli i negativne brojeve.
E sad, sta je poenta ove moje price? Pa drug i ja smo nesto razmisljali i dosli smo do zakljucka da ovaj skup (celih brojeva) NIJE beskonacan kao sto se to smatra samo zato sto to neko ne moze da objasni. Naime, kao sto i samo znate, ako se osvrnete oko sebe primeticete da je osnovni oblik u prirodi LOPTA, tj sve je zatvoreno samo u sebe. Na osnovu ove "teorije" ja smatram da su i SVI brojevi zatvoreni sami u sebe. Kada kazem SVI brojevi tu ubrajam CELE brojeve kao "osnovne" a tu su naravno i izmedju tih celih brojeva i racionalni, iracionali tj REALNI brojevi koji se (po meni) nalaze izmedju ovih CELIH brojeva.
Sad, zamislite jednu loptu i na njoj jednu tacku gde svi brojevi krecu, ja bih odabrao tacku 0 (koja ustvari i nije tacka, jer ja broj 0 ne smatram bas brojem vec odsustvom broja, kao sto je to slucaj kod crne boje, ali necu sada o tome) i od te tacke u jednu stranu krecu pozitivni brojevi a u drugu negativni. Posle nekog vremena oni ce se "susresti" na suprotnoj strani tacke 0 na toj nasoj zamisljenoj lopti i onda ce krenuti u suprotnu stranu. Jos samo treba otrkiti zakonitost te tacke koja ima veoma veliku vrednost (suprotnost od nule) i dokazacemo da su SVI brojevi konacni (u neku ruku).

E sad, odgovor na pitanje: iz ove teorije se zakljucuje da jos uvek ne mozemo da ogovorimo na to pitanje da li svih prirodnih brojeva ima isto koliko ima i parnih (ili neparnih) medju njima... sve dok se ne otkrije zakonitost !0 (ne nula) broja.

P.S. Mozda sam sada nalupetao tesku glupost ali eto, ponavljam, ja sam nevest matematicar ali imam bujnu mastu. Bice mi makar drago ako sam nekog nasmejao ovim postom. A jos draze ako sam podrzao jos neciju teoriju odavde sa foruma ili mozda nekog naucnika ( ) a samo da kazem da ja nisam upoznat sa nekim slicnim razmisljanjem.

P.S.2 Sada nesto razmisljam i bojim se da sam izostavio neki bitan deo u mojoj teoriji jer mi nesto tu ne stima?!?! Davno smo drug i ja mislili o ovome i tada nam je sve bilo jasno ko dan ali to nismo znali da objasnimo nikom drugom ili jos manje da stavimo na papir.

Da, tako to izgleda, ali ovo je činjenica:





Bijekcijom se svaki parni broj dvaput preslikava odnosno ima ga u dva para a on je jedan broj!!!





U jednom paru njemu se pridružuje neki broj, a u drugom paru on je pridružen nekom broju.
Da li je na osnovu broja ovako dobijenih parova ispravno doneti zaključak da parnih brojeva
ima isto toliko koliko i tih tako formiranih parova ili upola manje?



_{[Ovu poruku je menjao galet@world dana 19.12.2009. u 07:39 GMT+1]}

Dane, Dane... Matematičare jedan!

Ako uzmeš prirodne brojeve do ma koliko velikog ali KONAČNOG M, pa preslikavaš kako je već objašnjavano, tada NEMA bijekcije. Ovde zbilja ima M/2 parnih brojeva.
Ako uzmeš BESKONAČNO M tada IMA bijekcije. Kolikogod veliki broj K da uzmeš, postoji 2K pa ga možeš spariti sa K.

Suština je da nešto što je konačno može biti veliko koliko hoćeš ali da ima VEĆE od toga. To je kao neki fiksni broj, tačka na brojnoj osi.
Beskonačno je takođe veliko kolikogod hoćeš ali NEMA veće od toga. To je nešto kao funkcija, kao naš put u Evropu, taman misliš da si stigao a ono ima još...

Dane,

element a je preslikan u b znači da je elementu a pridružen element b, a ne obrnuto. Dakle, to ne znači da je b preslikan u a. Preslikati a u b znači elementu a pridružiti b. Original nije isto što i slika.

Da, bijekcijom je svakom prirodnom broju (pa i parnom) dodeljen paran prirodan broj po tačno jedanput. To znači da je uspostavljeno preslikavanje skupa N u 2N.

Pritom je svaki paran broj pridružen tačno jednom prirodnom. To znači da je uspostavljeno preslikavanje bijekcija.

U čemu je problem?

@Fitopatolog:


Matematika je natprirodna nauka. Ako malo razmisliš videćeš da je tako.

Ne, nije. Natprirodna je filozofija, samo ne znam da li je nauka?...

Pa matematika opisuje prirodu, nije DEO nje same,
kao sto mastilo ne sadrzi "plavu boju", vec je "plava
boja" samo posledica posmatranja nekog subjekta (coveka),
a zapravao kao takva nije sadrzana u samom
objektu (prirodi, mastilu).

Napravi skup prirodnih brojeva i kada ga pomnozish sa 2 dobices jedan paran broj za njega. 1, 2, 3, 4, 5... 1x2=2, 2x2=4, 3x2=6, 4x2=8, 5x2=10...

Ma, kakvu prirodu, to je formalna nauka primenljiva u drugim oblastima. Najosnovnija prirodna nauka je fizika.

Matematika ne opisuje prirodu, već apstraktne objekte, kao što je više puta rečeno. Matematika se nekada proučavala u okviru „matematičke grupe“ na Filozofskom fakultetu, jer je od svih nauka u najbližoj vezi sa Filozofijom (a zatim Filologijom).

Matematika filozofiji pruža formalnu osnovu.

Tvrditi da matematika opisuje prirodu isto je što i tvrditi da računari služe samo za računanje.

_{[Ovu poruku je menjao Cabo dana 20.12.2009. u 18:55 GMT+1]}

Ima li ovo veze sa temom?

Nedeljko, molim te!, isključi emocije i odgovori mi na ovo pitanje samo cifrom i bez komentara.

Uzmimo konačan skup od 100 prirodnih brojeva.

Koliko međusobno različitih parova parnih brojeva (iz tog skupa) možeš napraviti a da ti parovi nemaju ni jedan
zajednički element?

Očito, galet@world, odbijaš, kao i toliko puta dosad, da prihvatiš komentare ostalih kada ti skreću pažnju na to da bijekcija ne funkcioniše tako kako si je ti zamislio, a posebno da ništa nećeš postići posmatranjem konačnih skupova. Zbog svega toka, zaključavanje.