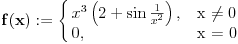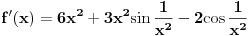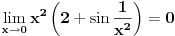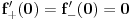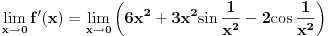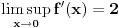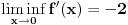[ Tosgin @ 21.12.2009. 22:18 ] @
|
[ miki069 @ 22.12.2009. 00:09 ] @
Ako je pitanje "nađi izvod date funkcije"?, onda:
Ti si izvod našao. Samo ga napiši alternativno kao i funkciju. Vrednost izvoda za x=0 jeste jednaka nula. Ako je pitanje "da li je diferencijabilna za X=0"?, onda: Zbog parnosti člana -2*cos(1/(x^2)) koji jedini ne teži nuli u limesu izvoda kada x teži 0, levi i desni limes su jednaki. Ali su oba neodređena. Vrednost izvoda za x=0 jeste jednaka nula. Oba limesa jesu jednaka ali ne zna se koliki su. Tako da...Ne znam. [Ovu poruku je menjao miki069 dana 22.12.2009. u 01:23 GMT+1] [ Tosgin @ 22.12.2009. 18:28 ] @
Hmm... Ako funkcija ima izvod u datoj tacki, onda je ona diferencijabilna u toj tacki, zar ne? Tako da mislim da se ne mogu odvojiti ta dva pitanja...
Citat: Vrednost izvoda za x=0 jeste jednaka nula. Oba limesa jesu jednaka ali ne zna se koliki su. Upravo to je i problem... Recimo da definisemo izvod date funkcije kao: 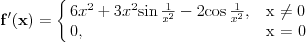 Tada, kako 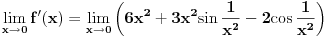 Ne postoji, slijedi da funkcija izvoda ima prekid za x = 0. (Ili je to pogresan zakljucak?) Ako izvod ima prekid u nekoj tacki, zar to ne znaci da tada funkcija nije diferencijabilna u toj tacki? [ Cabo @ 22.12.2009. 18:39 ] @
Tooo! Konačno malo „prave“ Analize.
Prvo, ova funkcija je neprekidna. Da li je i diferencijabilna? Izvod ove funkcije „podivlja“ u okolini nule („divlja“ i van te okoline, ali značajno manje — čitaj: „divljanje“ je konačno), što se da videti kada se nacrta njen grafik, npr. u programu Matematika. Problem je „dodefinisavanje“, jer se pri računanju izvoda fiksira tačka za koju se računa izvod. Funkcija bez dodefinisavanja nije diferencijabilna u nuli, jer joj izvod nije ograničen. Sa dodefinisavanjem, jedino dobiješ dodatnu zabunu jer ti odjednom izraz za levi i desni limes postanu nula u nuli. Poenta: niko nije rekao da i izvod mora da bude neprekidan. 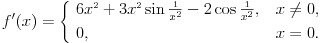 Funkcija je neprekidna (na celom svom domenu), diferencijabilna je u nuli, i izvod postoji u tački nula, kao i van nje, ali nije neprekidan. Case closed. [Ovu poruku je menjao Cabo dana 22.12.2009. u 19:58 GMT+1] [ miki069 @ 22.12.2009. 23:17 ] @
Vrste prekidnosti neke f-je su:
- OTKLONJIV PREKID: ako su levi i desni limes konačni i jednaki. Onda se može dodefinisati i biti neprekidna ta nova doddefinisana. - NOTKLONJIV PREKID: ako su levi i desni limesi konačni i nisu jednaki. - VERTIKALNA ASIMPTOTA: ako je bar jedan limes beskonačan Mislim da je Čabo u pravu 100%. Iako ih ne znamo (oba limesa "divljaju") znamo da su između sebe jednaki zbog parnosti i konačnosti "spornog" člana -2*cos(1/(x^2)). OTKLONJIV PREKID. Dosta dobar primer. Tosgin: je li ovo sa matematičkog fakulteta ili nekog tehničkog? [ Tosgin @ 22.12.2009. 23:19 ] @
Da funkcija nije dodefinisana, uopste ne bismo mogli traziti izvod u nuli jer ne bi pripadala domenu funkcije.
Nekako mi je tesko prihvatiti da je izvod definisan sa 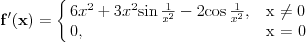 samo iz razloga sto je izvod takodjer funkcija. Da bi dodefinisali funkciju u nekoj tacki  , zar ne mora da bude: , zar ne mora da bude: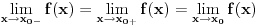 te se tada funkcija dodefinise kao: 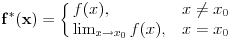 U ovom slucaju taj limes ne mozemo naci, tako da ne razumijem kako mozemo pisati da je vrijednost funkcije (tj. izvoda) u nuli -- nula. Citat: Funkcija je neprekidna (na celom svom domenu), diferencijabilna je u nuli, i izvod postoji u tački nula, kao i van nje, ali nije neprekidan. Da li ovo znaci da izvod ima prekid u nuli ili 'van nje'... Ne vidim kako bi se prekid mogao naci negdje drugo, a ako je u nuli, onda funkcija nema izvoda u nuli... :S Cini mi se da se samo vrtim u krug, ovdje, te da mi fali neki teoretski dio, ali sve sto sam nasao da ima veze sa prekidima izvoda je bila teorema o tackama prekida izvoda (i njene posljedice) ali se ona ne odnosi na ovu situaciju... Ako bi me neko mogao uputiti u pravom smjeru bio bih zahvalan. [Edit] Citat: Vrste prekidnosti neke f-je (ovde mislim na ovaj famozni izvod funkcije) su: - OTKLONJIV PREKID: ako su levi i desni limes konačni i jednaki. Onda se može dodefinisati i biti diferencijabilna. - NOTKLONJIV PREKID: ako su levi i desni limesi konačni i nisu jednaki. - VERTIKALNA ASIMPTOTA: ako je bar jedan limes beskonačan Mislim da je Čabo u pravu 100%. Iako ih ne znamo (oba limesa "divljaju") znamo da su između sebe jednaki. OTKLONJIV PREKID. Dosta dobar primer. Tosgin: je li ovo sa matematičkog fakulteta ili nekog tehničkog? Postao si dok sam ja pisao... ;) Eh, pa upravo to je stvar... mozemo zakljuciti da je prekid otklonjiv, ali ne znamo koja mu je vrijednost, te samim tim ne mozemo znati ni vrijednost izvoda u tacki nula? :D I, ne, nije matematicki fakultet, vec elektrotehnicki. [ Cabo @ 23.12.2009. 15:11 ] @
Citat: miki069: Čabo  Citat: Tosgin: Da funkcija nije dodefinisana, uopste ne bismo mogli traziti izvod u nuli jer ne bi pripadala domenu funkcije. Tačno. A osim toga, izvod se sve „brže“ menja što je vrednost argumenta bliža nuli. Citat: Tosgin:samo iz razloga sto je izvod takodjer funkcija. Da bi dodefinisali funkciju u nekoj tacki  , zar ne mora da bude: , zar ne mora da bude: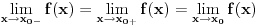 Mora, ali ne mora da bude i 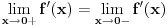 . Dodefinisana je funkcija . Dodefinisana je funkcija  , a ne funkcija , a ne funkcija 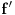 . .[ Nedeljko @ 23.12.2009. 20:08 ] @
Ovo je jedan od primera funkcije, koja je diferencijabilna na celom R, ali izvod nije neprekidan. Da, funkcija jeste diferencijabilna u nuli, to jest, izvod postoji na celom R, pa i u nuli. f' jeste definisano u nuli, ali nije neprekidno u nuli.
[ miki069 @ 23.12.2009. 20:42 ] @
Tosgin: je li ovaj zadatak sa kolokvijuma/pismenog/usmenog ili ti samo vežbaš?
Savo izvini. Svo vreme sam mislio da je Čabo. Prošarao si latinicu i ćirilicu. [ Tosgin @ 23.12.2009. 22:59 ] @
Da, shvacam sada... Prakticno se cijeli moj problem sveo na to da nisam znao da izvod funkcije moze imati prekid, a da je funkcija diferencijabilna na cijelom domenu... Hvala svima koji su odvojili vrijeme da ovdje odgovore.
@miki069; Ovo je bio dio zadatka za domacu zadacu. [ Nedeljko @ 24.12.2009. 07:24 ] @
Dodefinisanje bilo koje funkcije bilo kojom vrednošću u bilo kojoj tački u kojoj nije definisana je potpuno ispravna matematička konstrukcija. N aprimer, g(x)=1/x za x iz R\{0}, g(0)=17. Druga je stvar što funkcija g nije neprekidna, pa samim tim ni diferencijabilna u nuli.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|