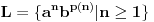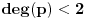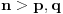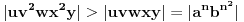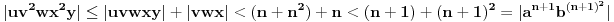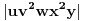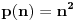[ japan @ 24.12.2009. 20:06 ] @
|
[ Goran Rakić @ 24.12.2009. 23:49 ] @
Koristi se lema o razrastanju za KS jezike (engl. pumping lemma) koja kaže da za svaki KS jezik
 postoje postoje 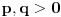 takvi da se svaka reč takvi da se svaka reč 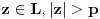 može zapisati kao može zapisati kao  gde gde  da za svako da za svako  važi važi  . .Dovoljno je pokazati da tvrđenje ne važi za 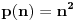 jer on pripada i klasama višeg stepena. Pretpostavljajući da jer on pripada i klasama višeg stepena. Pretpostavljajući da  jeste KS, po slučajevima kako sve jeste KS, po slučajevima kako sve  može da se podeli trebalo bi da dođe do kontradikcije u svakom slučaju. može da se podeli trebalo bi da dođe do kontradikcije u svakom slučaju.[Ovu poruku je menjao Goran Rakić dana 25.12.2009. u 11:45 GMT+1] [ Goran Rakić @ 25.12.2009. 00:30 ] @
[ Nedeljko @ 25.12.2009. 07:47 ] @
Neka je
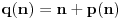 , ,  dužina pumpanja i dužina pumpanja i 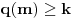 . Tada postoje reči . Tada postoje reči 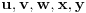 takve da je takve da je 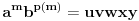 , , 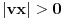 , , 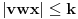 i tako da za ma koje i tako da za ma koje 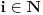 važi važi 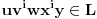 . .No, tada za svako 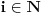 postoji postoji 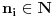 tako da je tako da je  , odakle je , odakle je  . Ukoliko je pak . Ukoliko je pak  polinom stepena bar dva sa pozitivnim vodećim koeficijentom, postojaće polinom stepena bar dva sa pozitivnim vodećim koeficijentom, postojaće 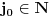 takvo da za sve takvo da za sve 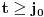 važi važi  , a samim tim i , a samim tim i 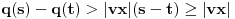 za za 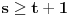 . Tada će takođe za . Tada će takođe za 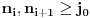 biti ispunjeno biti ispunjeno  , pa za , pa za  i i 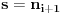 imamo kontradikciju. imamo kontradikciju.[ japan @ 25.12.2009. 10:11 ] @
Citat: Goran Rakić: Dovoljno je pokazati da tvrđenje ne važi za 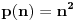 jer on pripada i klasama višeg stepena. jer on pripada i klasama višeg stepena.Ovo je ključna stvar. Ja sam sve vreme pokušavao da dokažem da tvrđenje ne važi za polinom opšteg oblika 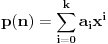 , što mi nikako nije uspevalo. , što mi nikako nije uspevalo.Hvala puno. [ Nedeljko @ 25.12.2009. 11:54 ] @
Pa, dao sam dokaz za opšti polinom stepena bar dva.
[ japan @ 25.12.2009. 12:19 ] @
[ Nedeljko @ 25.12.2009. 18:46 ] @
A ja sam stavio komentar da nije ta činjenica ključna, jer se može pokazati i bez nje. OK, olakšava posao, mada meni i dalje nije jasno kako se opšti slučaj svodi na taj.
[ Goran Rakić @ 25.12.2009. 19:41 ] @
Da, izgleda da sam se ja ipak zaleteo. Stepen polinoma traži ne-nula koeficijent uz vodeći član. Moje "rešenje" samo pokazuje da L nije KS za polinome stepena 2 što je uže tvrđenje.
Hajde da pokušam da ispravim, može se posmatrati polinom 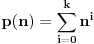 stepena k. stepena k.Dalje po binomnoj formuli 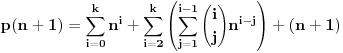 . .Za 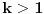 uz uz 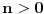 dobija se druga nejdnakost potrebna za kontradikciju da je napumpana reč duža od dobija se druga nejdnakost potrebna za kontradikciju da je napumpana reč duža od 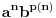 , a kraća od , a kraća od  . .[Ovu poruku je menjao Goran Rakić dana 25.12.2009. u 21:28 GMT+1] [ Nedeljko @ 25.12.2009. 21:23 ] @
Po Lagranževoj teoremi o srednjoj vrednosti je q(n+1)-q(n)=q'(c) za neko c iz intervala (n,n+1). Obzirom da za polinom q stepena bar 2 sa pozitivnim vodećim koeficijentom q'(x) teži beskonačnosti kad x teži beskonačnosti, počev odnekle će biti q'(x)>k, kolika god da je konstanta k, pa skup svih q(n), gde n ide preko N, neće moći da obuhvati nijedan odozgo neograničen aritmetički niz, a po pumpiung lemi bi morao.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|