[ milutinovicsm @ 28.12.2009. 11:06 ] @
| Da li bi mi neko mogao pomoci oko ovog zadatka:Odrediti skup svih realnih vrednosti parametra a za koje nejednacina x^2-a(a+1)+a^3 <=0,ima tacno 5 celobrojnih resenja. |
|
[ milutinovicsm @ 28.12.2009. 11:06 ] @
[ Cabo @ 28.12.2009. 12:48 ] @
[ Farenhajt @ 28.12.2009. 12:54 ] @
Cabo, proradila ti je slepa mrlja. Posredi je kvadratna NEjednačina.
[ Cabo @ 28.12.2009. 13:00 ] @
[ milutinovicsm @ 28.12.2009. 16:00 ] @
A cekaj,odakle ti to? :-)
[ miki069 @ 28.12.2009. 23:15 ] @
Zbunio te je sa Lamda1 i Lambda2.
Misli na X1 i X2. Pošto ti je vodeći koeficijent ispred X^2 pozitivan (+1) kvadratna funkcija je <= nuli na intervalu od uključno X1 do uključno X2. Taj interval je dugačak ABS(X2 - X1) (ABS je apsolutna vrednost) što ne mora biti ceo broj, pa je SAVO to ubacio u funkciju "ceo deo" INT(ABS(X2 - X1)) da bi dužina postala celobrojna. Razlika X2 - X1 bi trebalo da izađe koren(D) gde je D diskriminanta. Izrazi je preko parametra a i vodi računa da mora da bude D>0. ABS funkciju možeš i sam da skineš, a zajedno ćemo da se molimo za INT funkciju kako da je skinemo. SAVO to radi na dosta visokom nivou - klasičan matematičar. [Ovu poruku je menjao miki069 dana 29.12.2009. u 00:29 GMT+1] [ Cabo @ 29.12.2009. 13:11 ] @
Citat: miki069: SAVO to radi na dosta visokom nivou - klasičan matematičar. LOL Još nisam matematičar. Ali da, lepo si opisao, programerski, šta se dešava u zadatku. Inače, oznaka  se koristi kod Gojka Kalajdžića iz Algebre 1 da označi nulu polinoma. se koristi kod Gojka Kalajdžića iz Algebre 1 da označi nulu polinoma. U principu, možeš ti da kažeš i 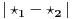 , ista ti je stvar. , ista ti je stvar.[ Nedeljko @ 29.12.2009. 15:30 ] @
[ milutinovicsm @ 29.12.2009. 23:46 ] @
Hvala :-) Posto mi nije bas najjasnije kako ste uopste dosli do toga,buduci da sam ja samo uspeo da odredim diskriminantu i da dobijem interval za X po a,da li imate kojim slucajem volje da mi objasnite postupak nalazenja a?
[ Nedeljko @ 30.12.2009. 00:32 ] @
Mrzi me, ali kada niko drugi neće, moraću ja.
Rešenja odgovarajuće kvadratne jednačine su  i i 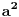 . Jasno je da iz . Jasno je da iz 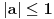 sledi sledi 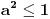 , pa je skup rešenja širine ne veće od 2, pa ne može sadržati 5 celih brojeva. , pa je skup rešenja širine ne veće od 2, pa ne može sadržati 5 celih brojeva.Za 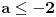 skup rešenja svakako obuhvata najmanje 7 celih brojeva - -2,-1,0,1,2,3,4, a za skup rešenja svakako obuhvata najmanje 7 celih brojeva - -2,-1,0,1,2,3,4, a za 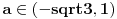 , može obuhvatati eventualno -1,0,1,2, dok za , može obuhvatati eventualno -1,0,1,2, dok za 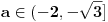 obuhvata upravo -1,0,1,2,3. obuhvata upravo -1,0,1,2,3.Za 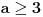 je interval rešenja širine najmanje 6, pa obuhvata više od 5 celih brojeva. Za je interval rešenja širine najmanje 6, pa obuhvata više od 5 celih brojeva. Za 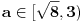 obuhvata cele brojeve 3,4,5,6,7,8. Za obuhvata cele brojeve 3,4,5,6,7,8. Za 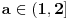 interval rešenja je širine manje od 4, pa ne može obuhvatati 5 celih brojeva. Za interval rešenja je širine manje od 4, pa ne može obuhvatati 5 celih brojeva. Za 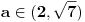 obuhvata eventualno cele brojeve 3,4,5,6. Za obuhvata eventualno cele brojeve 3,4,5,6. Za 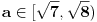 obuhvata cele brojeve 3,4,5,6,7. obuhvata cele brojeve 3,4,5,6,7.[ Cabo @ 30.12.2009. 15:17 ] @
Citat: Nedeljko: Ama, rešenje je 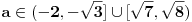 . Još kada bi neko obrazložio kako treba. . Još kada bi neko obrazložio kako treba.Vidiš, Cabo, ceo deo od  je 4, ali interval (0.9,5.1) obuhvata čak 5 celih brojeva itd. je 4, ali interval (0.9,5.1) obuhvata čak 5 celih brojeva itd.Ja nisam rekao ceo deo. Ja sam rekao 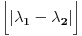 . .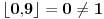 . .Dobro, shvatam, 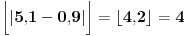 . . Onda samo dodam jedan: 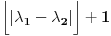 . . Pih, kao u programiranju, kad ne mogu nikako da pogodim da li niz počinje od 0 ili 1. [ Nedeljko @ 30.12.2009. 21:47 ] @
[ Cabo @ 30.12.2009. 22:23 ] @
Pa da, dakle, ponoviću: dodajem jedan. :-]
[ Nedeljko @ 31.12.2009. 08:08 ] @
Dao sam ti primer koji pokazuje da broj celih brojeva u zatvorenom intervalu nije funkcija širine intervala. Ako ti i dalje nije jasno
|1.9-0.1| = 1.8 = |2.2-0.4|. Interval [0.1,1.9] sadrži samo jedan ceo broj, a [0.4,2.2] dva cela broja. Možeš ti da dodaješ i oduzimaš šta hoćeš, ali broj celih brojeva u zatvorenom intervalu nije funkcija njegove širine. [ Cabo @ 31.12.2009. 18:11 ] @
Mislim da si donekle u pravu. „Greška“ je ograničena. Nekad se dodaje jedan, a nekad ne.
[ miki069 @ 01.01.2010. 19:52 ] @
"broj celih brojeva u zatvorenom intervalu nije funkcija njegove širine. " Tačno.
Ali jeste od X1 i X2. broj = ABS(INT(X2) - INT(X1)) Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|