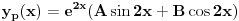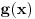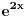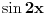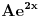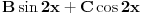[ mungosss @ 30.12.2009. 00:28 ] @
| Jedno pitanje. Ako su ovo opsta resenja kako glase diferencijalne jednacine od ovih opstih resenja? y = e^x (C1 sin 2x + C2 cos 2x) ovde sam dobio y''-2y'+5y=0 to je valjda ok y = C1 e^2x + C2 e^(-2x) + x^2. al ovde bas ne znam kako da postavim za partikularno i sta bi islo sa desne strane? Hvala! |