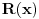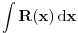[ mungosss @ 30.12.2009. 16:41 ] @
| Da li neko zna da resi y' +(x^2)sinx=xy , dobijem u jednom delu integral od (x^2)sinx*e(-x^2/2) , sto ne znam da l moze da se resi? U zadatku (y^2)y'=2x^2 + y^2 + xy takodje dobijem integral od 1/(2x^4 + x^3 + x^2 -x) ,ne znam da l moze da se resi i ovaj integral ? |