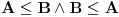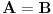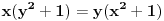Treba samo da nađeš kontra primer. Pokušaj sa x = 0, y = -1

U stvari treba da se pokaze da iz ovih nejednacina na R ne sledi x=y, jer mi se to javlja kod antisimetricnosti, nisam bas lepo napisao, sorry. Pa ne znam dal bi moglo tako da se dokaze.

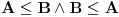
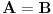
Dakle, sistem je oblika , što je ekvivalentno sa , pa prema tome imaš jednačinu



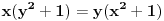
Sad malo prebaci sve na jednu stranu, rastavi na činioce i vidi do kakvog zaključka dolaziš.

FArenhajt to sam i radio, inace tako uvek dodjem do resenja medjutim ovde dobijem xy^2 + x -yx^2-y=0 i sa tim ne mogu bukvalno nista da uradim.

Kao što gore rekoh, možeš da rastaviš na činioce.

Svaka tebi cast, ali ne znam kako bih to izveo.

(1-xy)(x-y)=0

Jao da, hvala! Samo sto je problem sto na (1,+beskonacno) treba da se dobije da je x=y,tj. da je antisimetricna,a na R da nije x=y. TAman sam mislio da sam dokazao da na (1,+besk) mora biti x=y kad ono sad ispade da moze biti i x=1/y.
Mada kad bolje razmislim znaci ne moze biti razlomak na (1,+beskonacno) sto znaci da mora biti x=y.A na R imamo dve mogucnosti x=y i x=1/y, sto znaci da ne mora biti x=y pa na R nije antisimetricna a na (1,+beskonacno) jeste. Valjda je tako!

Hvala puno jos jednom!