[ zoran_ets @ 06.01.2010. 17:12 ] @
| imam problem oko resavanja ove jednacine |-x|-1=0 |
|
[ zoran_ets @ 06.01.2010. 17:12 ] @
[ zoran_ets @ 06.01.2010. 17:20 ] @
ja sam postavio ovako
|-x|= ( -x,-x>=0,x<=0 ) i ( -(-x),-x<0,x>0 ) i dalje sam dobio resenja kada x<=0 x=-1 i kada je x>0 x=1, zanima me da li se posmatra samo uslov kada je x<=0,jer bi tada |-x|=-x [ Gn0m3 @ 06.01.2010. 17:23 ] @
Apsolutna vrednost u suštini znači da trebaš da razmotriš dva slučaja:
1. -x > 0 => x < 0 -x - 1 = 0 -x = 1 x = -1 2. -x < 0 => x > 0 - (- x) - 1 = 0 x - 1 = 0 x = 1 Pošto me preteče, da naglasim još jednom - razmatraš oba slučaja. Nije tu apsolutna vrednost slučajna. :) [ zoran_ets @ 06.01.2010. 17:25 ] @
da razumem to ,ali evo cele jednacine ||x-1|-1|-1=0
potrebno je da se izracunaju sva resenja a posle izracunavanja da se rezultati saber resenje je 3, a sa ovim rezultatima je 4...? [ Cabo @ 06.01.2010. 17:51 ] @
[ zoran_ets @ 06.01.2010. 18:25 ] @
ne razumem...iskreno,ali ja mislim ipak da je zbir ,jer su ponudjena resenja,3,5,2,a 4 uopste nije ponudjeno
[ Gn0m3 @ 06.01.2010. 18:44 ] @
Naime, prvo posmatramo "najunutrašnjiju" apsolutnu vrednost
1. x - 1 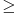 0 => x 0 => x 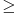 1 1|x - 1 - 1| - 1 = 0 |x - 2| - 1 = 0 1.a. x - 2 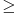 0 => x 0 => x 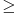 2 2x - 2 - 1 = 0 x = 3 1.b. x - 2 < 0 => x < 2 -x + 2 - 1 = 0 x = 1 2. x - 1 < 0 => x < 1 |-x + 1 - 1| - 1 = 0 |-x| - 1 = 0 2.a. -x 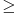 0 => x 0 => x 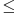 0 0-x - 1 = 0 x = -1 2.b. -x < 0 => x > 0 -(-x) - 1 = 0 x - 1 = 0 x = 1 Vrednost za 2.b. nije rešenje (dobili smo 1 a predpostavili smo da je x < 1) te je stoga zbir 3 + 1 - 1 = 3 Nadam se da ti je sad jasnije :) [Ovu poruku je menjao Gn0m3 dana 06.01.2010. u 21:32 GMT+1] [Ovu poruku je menjao Gn0m3 dana 06.01.2010. u 23:03 GMT+1] [ Farenhajt @ 06.01.2010. 19:15 ] @
[ zoran_ets @ 06.01.2010. 19:29 ] @
ok dobili smo ista resenja,ali me nesto buni:
meni je profesorka objasnjavala da npr. |x+1| je x+1 kada je x+1 >= 0 a kada ima - ispred oda je manje od nule (-(x+1),i onda je x+1<0) e a u ovom slucaju imamo komplikaciju zato sto je -x,o cemu pricam,,, kada neku nejednacinu tj npr. -x-1>0 pomnozimo sa -1 okrenuce se znak, a x uvek mora na kraju da bude pozitivan ,e ako posmatras |-x|moze da bude= ( -x,-x>=0,x<=0 menjamo znak ) i ( -(-x),-x<0,x>0 menjamo znak ) ,i onda dolazi do promene znaka... verovatno si upravu,ali zasto mi je profesorka govorila o ovome? a ako uzmem u obzir samo manje brojeve od nule zato sto je -x onda i ja dobijem resenje... (verovatno ces reci "pa sto onda ne pitas profesrku" ,logicno zar ne?,ali jos traje raspus) hvala puno na ulozenom trudu... razumem te potpuno sta pricas ali jednostavno mi se sve pomesalo,pa ne znam sta je pravilno.... [ zoran_ets @ 06.01.2010. 19:35 ] @
e kod linearnih funkcija kada sam pokusavo da resim zadatako koji je bio slican(y=|3-|x-2||) ovome ,isao sam spolja i pogresio sam ,dobio sam grafik koji je apsurdan...(vise puta sam proveravao),e onda sam postavio temu i lik mi je rekao prvo da resi unutrasnju pa da resavavm spoljnu... ne razumem u cemu je fora.da li je sve jedno koju prvo resavam zagradu?
[ Gn0m3 @ 06.01.2010. 19:48 ] @
Imam utisak da si pogrešno shvatio profesorku :)
Apsolutna vrednost je u suštini skraćen zapis sledećeg: 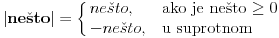 Neka te ne buni to što u apsolutnoj vrednosti stoji -x. To nikako ne znači da je x nužno negativan. Prema ovom što sam rekao 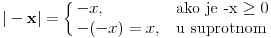 i to je sve. Nikakva dalja filozofija :) @Farenhajt: Jbga, posle matematičkog prirodno mi dolazi da tražim rekurzivne algoritme kad je god to moguće :D Zato uvek krećem od najunutrašnjije. @zoran_ets: U suštini, svejedno je da li krećeš od najspoljašnije ili najunutrašnjije apsolutne vrednosti - svejedno ćeš dobiti tačan rezultat. Jedino moraš da uvek imaš na umu šta apsolutna vrednost zapravo znači [ dobar_decko @ 06.01.2010. 20:11 ] @
A zasto nismo pretpostavili da je x<=1 ?
Uopste,kod ovakvih slucajeva,kada smes da ukljucis granicnu vrednostu? U ovom slucaju,zasto ti uslovi nisu X>=1 ili X<=1 ? [ Gn0m3 @ 06.01.2010. 20:30 ] @
Nismo pretpostavili da je
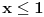 , jer ne smemo to da pretpostavimo, a to smemo na predpostavimo pošto to nije u skladu sa definicijom apsolutne vrednosti. Definicija apsolutne vrednosti je u mom postu iznad. , jer ne smemo to da pretpostavimo, a to smemo na predpostavimo pošto to nije u skladu sa definicijom apsolutne vrednosti. Definicija apsolutne vrednosti je u mom postu iznad.Istini za volju, napravio sam štamparsku grešku u rešavanju pošto sam pisao > a ne 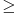 , ispraviću ga korektnosti radi. , ispraviću ga korektnosti radi. [ dobar_decko @ 06.01.2010. 20:35 ] @
Znaci kod apsolutnih vr. se u uslovima ne ukljucuju vrednosti?
[ dobar_decko @ 06.01.2010. 20:41 ] @
A pod 1 b dobijes 1 a u uslovu pod 1 dobijas da je x>1?
Zasto sada ovo uzimas kao resenje? [ dobar_decko @ 06.01.2010. 20:44 ] @
Jos nesto...
U slucaju 1. imas jedan uslov,u slucaju 1. a imas drugi uslov,da li onda moras da radis njihov presek,i da na osnovu njega proveris da li uzimamo resenje koje dobijemo pod 1. a? [ Gn0m3 @ 06.01.2010. 22:15 ] @
Citat: dobar_decko: Znaci kod apsolutnih vr. se u uslovima ne ukljucuju vrednosti? Uključuju se kad razmatramo slučaj 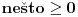 kao što lepo piše u definiciji :) Inače ne. Nisam svuda bio ispravio grešku, to te je najverovatnije zbunilo :) Citat: dobar_decko: U slucaju 1. imas jedan uslov,u slucaju 1. a imas drugi uslov,da li onda moras da radis njihov presek,i da na osnovu njega proveris da li uzimamo resenje koje dobijemo pod 1. a? Slučaj 1.a. jeste upravo presek dva uslova. [ zoran_ets @ 07.01.2010. 17:23 ] @
||x-1|-1|-1=0
|x-1|moze biti x-1,x-1>=0,x>=1 i -(x-1),x-1<0,x<1 imamo dva uslova : *prvi x<1 i tu: |-x+1-1|-1=0 |-x|-1=0 e sada |-x| moze da bude= ( -x,-x>=0,x<=0 menjamo znak ) i ( -(-x),-x<0,x>0 menjamo znak ) e tu imamo dva uslova: **x<=0 i tu je -x-1=0,-x=1,x=-1 (kada se odradi presek prvog uslova i ovog dobije se uslov da svi brojevi mooraju da budu manji od 1 al ne ukljucujuci 1) **x>0 i tu je :x-1=0,x=1( a kada se odradi presek dobije se da brojevi idu od nule do 1 ali bez 1, pa se ne uzima ovo resenje) *drugi uslov je:x >=1 |x-1-1|-1=0 |x-2|-1=0 |x-2| moze da bude x-2,x-2>=0,x>=2 i -(x-2),x-2<0,x<2 pa imamo dva uslova : **prvi x<2 tu je : -x+2-1=0 -x+1=0 x=1 (kada se odradi presek brojevi idu od 2 do 1 ali ukljucuje 1) **drugi x>=2 x-2-1=0 x=3(prema preseku brojevi treba da budu veci ili jedanaki sa 2) [ Zoran Pantic @ 06.02.2010. 18:54 ] @
2∙8^x-7∙4^x+7∙2^x-2=0 ...rec je o eksponencijalnoj jednacini ..
resio sam 20-tak zd i dosa do ovog... ne znam kako rastaviti 8^x ... ako neko zna kako uraditi ovaj zd nek' kaze ..molim vas ...treba mi to za pon :S unapred Hwala [ Zoran Pantic @ 06.02.2010. 18:57 ] @
2∙8^x-7∙4^x+7∙2^x-2=0 ...rec je o eksponencijalnoj jednacini ..
resio sam 20-tak zd i dosa do ovog... ne znam kako rastaviti 8^x ... ako neko zna kako uraditi ovaj zd nek' kaze ..molim vas ...treba mi to za pon :S unapred Hwala [ Zoran Pantic @ 06.02.2010. 20:24 ] @
hwala puno ... :D ..al u medjuveremnu sam to skontao :D .... i kasnije pomocu simetricne jednacine treceg stepena.... ;) thx
sad sam dosao do poslednjeg al ima probl... dobijem t1=13 :S ..a 13 se ne moze rastaviti emm ne mogu napisati ZD kak treba s korenima.. .. :S [ Zoran Pantic @ 06.02.2010. 20:26 ] @
√(3^x-5)+√(3^(x+1)-11)=6 owak nekako ... to sto je u "()" je ustavati pod korenom
[ zzzz @ 06.02.2010. 22:34 ] @
[ Zoran Pantic @ 06.02.2010. 22:53 ] @
√(3^(x+1)-11) ----- (x+1) a ti racunar bez tog +1 ? :S
[ zzzz @ 06.02.2010. 22:59 ] @
(3^(x+1)=3^x*3^1
[ Zoran Pantic @ 06.02.2010. 23:21 ] @
OK ... hwala puNoo ... pokusat cu resiti ...javim sutra jesam li resio..sad odo spawati.... HWala josh jednom
[ Zoran Pantic @ 07.02.2010. 11:42 ] @
drug, ne moze se resiti... pokusaj ti izracunati t1/2=? pa ces videti? :S
[ Nedeljko @ 07.02.2010. 13:02 ] @
[ Zoran Pantic @ 07.02.2010. 13:29 ] @
a kako dodje do te jednacine ... ja ne mogu dobiti takaw oblik ??
[ Zoran Pantic @ 07.02.2010. 13:55 ] @
[ Zoran Pantic @ 07.02.2010. 15:09 ] @
Hvala ljudi... resio sam zd. kako mogu upload sliku da vidite kak ide ? // ne bih rekao da je tako heh
[ Zoran Pantic @ 07.02.2010. 19:32 ] @
[ Zoran Pantic @ 07.02.2010. 20:21 ] @
hehe ja sam II sr. i josh uvek nisam radio log. ;) to treba naredna oblast da bude ... ;) ... a imas uslov... i ne zadovoljava ...t1 ne zadovoljava uslov
[ Nedeljko @ 07.02.2010. 20:59 ] @
Pravilno ga je odbacio. Uostalom, proveri. Neće biti 22=6.
[ Zoran Pantic @ 07.02.2010. 21:01 ] @
[ zzzz @ 07.02.2010. 21:11 ] @
OK. nisi učio log pa netrebaš tražiti x.Ali kakav si to uslov izmislio
i zašto? Mogao si napisati nešto ovako: 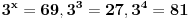 pa je x neki broj veći od 3, a manji od 4. Učili ste valjda da eksponent ne mora biti prirodan broj.Naprimjer 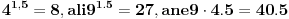 ---------------------- OK. Kad sam ja išao u srednju vrijedilo je pravilo da drugi korijen ima dva rješenja, treći korijen tri rješenja itd. Poštujem nove zakone. [ Zoran Pantic @ 07.02.2010. 21:26 ] @
"Kad sam ja išao u srednju vrijedilo je pravilo da drugi korijen ima dva rješenja, treći korijen tri rješenja itd." josh uvek to vredi..al ok..hwala Vam...ZD je resen :D [ Nedeljko @ 08.02.2010. 10:19 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|