Pošto dugo vremena nije bilo odgovora na temu, evo dajem rješenje, nadam se da je tačno :)

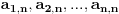
Za svako definišimo na sledeći način:

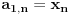
1. , i
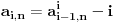
2. , za .

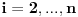
Tada imamo da je:



...

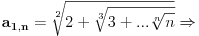
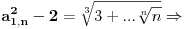
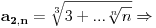
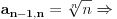
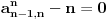
, tj.
.

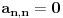
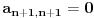
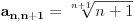
Tada je i , odakle je , pa je:
.

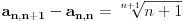
Sređujući lijevu stranu gornje jednakosti dobijamo:




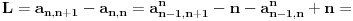
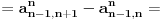
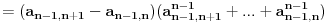
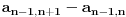
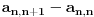
Dalje, kad sredimo na sličan način kao što smo gore sredili , i tako dalje, dobijamo konačno:





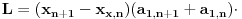
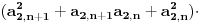
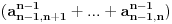
Odnosno, ako uvedemo smjenu :
,
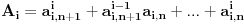
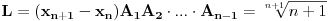
pa je:


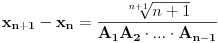
A onda je:





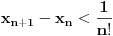
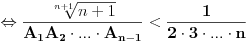
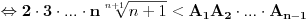
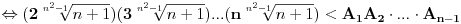
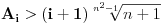
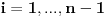
Dokazaćemo da je , za iz čega sledi gornja nejednakost.
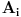
Primjenom nejednakosti aritmetičke i geometrijske sredine na imamo:


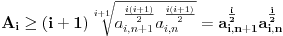
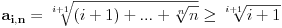
Pošto je i
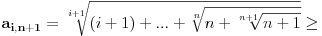
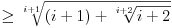
, imamo da je:
.

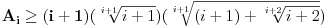
Onda:


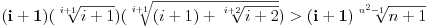
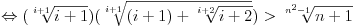
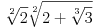
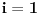
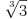
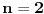
Lijeva strana ima najmanju vrijednost za , što se može dokazati indukcijom ili analitički, a desna ima najveću vrijednost za , pa je gornja nejednakost tačna, a iz nje slijedi i nejednakost .
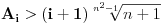