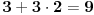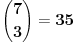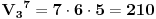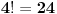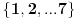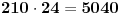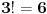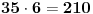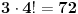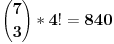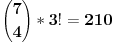Kada iz takve permutacije izbaciš fiksne tačke, dobijaš permutaciju od 4 elementa (označićemo ih sa 1,2,3 i 4) bez fiksnih tačaka. Imaš dve vrste takvih permutacija: proizod dve nezavisne transpozicije (određena slikom prvog elementa) i ciklus dužine 4 (određen slikom jedinice i slikom slike jedinice). Ukupno ih ima Pomnoži to sa i dobićeš konačan rezultat 315.

Nedeljko, da li mi možeš pojasniti ovaj dio!?

"Imaš dve vrste takvih permutacija: proizod dve nezavisne transpozicije (određena slikom prvog elementa) i ciklus dužine 4 (određen slikom jedinice i slikom slike jedinice). Ukupno ih ima 3 + 3*2= 9" , može li se ikako objasniti bez ovih "slika"

ja sam uaradio kao i "number22", nije mi jasno što ne može tako!! :/

_{[Ovu poruku je menjao Janko666 dana 09.02.2011. u 13:04 GMT+1]}

Pozicije u permutacijama na kojima su raspoređeni fiksirani elementi biramo proizvoljno i fiksiramo. 3 elementa skupa se mogu na datim pozicijama fiksirati na načina. Preostala četiri elementa skupa, koji nisu raspoređeni, mogu se rasporediti na načina. Koje god druge pozicije da ponovo uzmemo i fiksiramo, permutacije su sadržane u prethodnima.

Traženi broj permutacija sa tacno tri fiksirana elementa skupa je .

Na 35 nacina mozes izabrati tri fiksne tacke u datom skupu. A preostale 4 cifre u permutaciji ne smiju imati f.tacku. Pa ti odgovaraju samo: tri proizvoda transpozicija (12)(34), (13)(24), (14)(23) i sest ciklusa duzine 4 (1234), (1243), (1324), (1342), (1423), (1432) posto je na taj nacin onemogucena f.tacka. Pomnozis i dobijes 315

Tačno. Ali svake od tri fiksne tačke mogu da se rasporede na različitih načina, tako da možeš da ih fiksiraš na različitih načina.




To je jasno.

Kad izaberes f.tacke one su vec rasporedjene. Pa ako pocnes da ih rasporedjujes onda vise nisu f.tacke

"Kome sad, kome da verujem. . . " xD

Vidanu:)

Fiksirajmo onda tri tačke. Broj permutacija sa fiksirane te tri tačke je .

A Vidan je !?

Fiksna tacka permutacije se dobija tako sto na i-to mjesto u permutaciji stavis broj i. U ovom slucaju 1 na prvom mjestu ili 2 na drugom itd. je f.tacka. Pa tri f.tacke mozes odabrati na 35 nacina u datom skupu

Evo sve super objasnjeno::http://www.math.umn.edu/~garre...pto/Overheads/06_perms_otp.pdf

Skup A "Bar 3 fiksne tačke" ima kardinalitet:
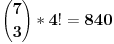
Skup B "Bar 4 fiksne tačke" ima kardinalitet:
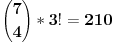
Tačno 3 fiksne tačke se dobija oduzimanjem kardinaliteta skupova A i B, to jest 840-210 = 630.
630 je netačno i duplo je više od tačnog Nedeljkovog rešenja 315. To je možda samo slučajnost, a možda i ima neka veza.
315 je tačno rešenje, ali ge ne razumem ni posle objašnjena koje je dao Number22.
Razumem ga "na prste" u konkretnoj situaciji:
Neka su fiksni 1,2,3 na prva 3 mesta onda od ostatka skupa, da ne bi bilo 4-og fiksa ne može 24 permutacije već samo sledećih 9 permutacija:
5476
5674
5746

6574
6745
6754

7456
7645
7654

Ne razumem kako je tako lako izbrojano 9 permutacija.
Na prste ne pije vodu za recimo 20 elemenata i 8 fiksnih tačaka.
Može li neko pojašnjenje transpozicija slike i slikine slike..
Interesuje me i gde je greška u logici preko kardinaliteta: 840-210=630

_{[Ovu poruku je menjao miki069 dana 10.02.2011. u 17:19 GMT+1]}

Ne trazi se bar nego tacno 3 fiksne tacke.

Jasno mi je to.
Zato sam od "najmanje 3" (840) oduzimao "najmanje 4" (210) i dobio 630.
Nije mi jasno zašto "najmanje 3" minus "namanje 4" ne daje "tačno 3"?
A trebalo bi.

Jasno mi je i da je 315 tačan rezultat.
315 = 35*9.
Nije mi jasno kako je Nedeljko "izbrojao" ovih 9 na 4 mesta.

Moze i preko formule za besporedak (rastroj poretka).
Suma od (-1)^k * (n nad k) * (n-k)! ; k ide od nula do n. U ovom slucaju za n=4 se dobije 9.
A na onaj nacin se dobija pogresan rez jer se ponavljaju permutacije sa 4,5,6,7 fiksnih tacaka za razlicite izbore 3 f.tacke

Sve razumeo.
Hvala number22.